NCERT Mathematics Question Paper (Class - 11)

---

(Mathematics) : Chapter 1 Sets

---

EXERCISE 1.1

Question 1. Which of the following are sets ? Justify your asnwer.

(i) The collection of all the months of a year beginning with the letter J.
(ii) The collection of ten most talented writers of India.
(iii) A team of eleven best-cricket batsmen of the world.
(iv) The collection of all boys in your class.
(v) The collection of all natural numbers less than 100.
(vi) A collection of novels written by the writer Munshi Prem Chand.
(vii) The collection of all even integers.
(viii) The collection of questions in this Chapter. (ix) A collection of most dangerous animals of the world.

Question 2. Let A = {1, 2, 3, 4, 5, 6}. Insert the appropriate symbol ∈ or in the blank spaces:

(i) 5. . .A
(ii) 8 . . . A
(iii) 0. . .A
(iv) 4. . . A
(v) 2. . .A
(vi) 10. . .A

Question 3. Write the following sets in roster form:

(i) A = {x : x is an integer and –3 < x < 7}
(ii) B = {x : x is a natural number less than 6}
(iii) C = {x : x is a two-digit natural number such that the sum of its digits is 8}
(iv) D = {x : x is a prime number which is divisor of 60}
( v) E = The set of all letters in the word
(vi) F = The set of all letters in the word

Question 4. Write the following sets in the set-builder form :

(i) (3, 6, 9, 12}
(ii) {2,4,8,16,32}
(iii) {5, 25, 125, 625}
(iv) {2, 4, 6, . . .} (v) {1,4,9, . . .,100}

Question 5. List all the elements of the following sets :

(i) A = {x : x is an odd natural number}
(ii) B = {x : x is an integer, 1 2 – < x 9 2 }
(iii) C = {x : x is an integer, x2 ≤ 4}
(iv) D = {x : x is a letter in the word “LOYAL”}
(v) E = {x : x is a month of a year not having 31 days}
(vi) F = {x : x is a consonant in the English alphabet which precedes k }.

Question 6. Match each of the set on the left in the roster form with the same set on the right described in set-builder form:

(i) {1, 2, 3, 6} (a) {x : x is a prime number and a divisor of 6}
(ii) {2, 3} (b) {x : x is an odd natural number less than 10}
(iii) {M,A,T,H,E,I,C,S} (c) {x : x is natural number and divisor of 6}
(iv) {1, 3, 5, 7, 9} (d) {x : x is a letter of the word MATHEMATICS}.

EXERCISE 1.2

Question 1. 1Which of the following are examples of the null set]

(i) Set of odd natural numbers divisible by 2
(ii) Set of even prime numbers
(iii) { x : x is a natural numbers, x < 5 and x > 7 }
(iv) { y : y is a point common to any two parallel lines}

Question 2. Which of the following sets are finite or infinite

(i) The set of months of a year
(ii) {1, 2, 3, . . .}
(iii) {1, 2, 3, . . .99, 100}
(iv) The set of positive integers greater than 100
(v) The set of prime numbers less than 99

Question 3. State whether each of the following set is finite or infinite:

(i) The set of lines which are parallel to the x-axis
(ii) The set of letters in the English alphabet
(iii) The set of numbers which are multiple of 5
(iv) The set of animals living on the earth
(v) The set of circles passing through the origin (0,0)

Question 4. In the following, state whether A = B or not:

(i) A = { a, b, c, d } B = { d, c, b, a }
(ii) A = { 4, 8, 12, 16 } B = { 8, 4, 16, 18}
(iii) A = {2, 4, 6, 8, 10} B = { x : x is positive even integer and x ≤ 10}
(iv) A = { x : x is a multiple of 10}, B = { 10, 15, 20, 25, 30, . . . }

Question 4. Are the following pair of sets equal ? Give reasons.

(i) A = {2, 3}, B = {x : x is solution of x2 + 5x + 6 = 0}
(ii) A = { x : x is a letter in the word FOLLOW} B = { y : y is a letter in the word WOLF}

Question 5. From the sets given below, select equal sets : A = { 2, 4, 8, 12}, B = { 1, 2, 3, 4}, C = { 4, 8, 12, 14}, D = { 3, 1, 4, 2} E = {–1, 1}, F = { 0, a}, G = {1, –1}, H = { 0, 1}

EXERCISE 1.3

Question 1. Make correct statements by filling in the symbols ⊂ or in the blank spaces :

(i) { 2, 3, 4 } . . . { 1, 2, 3, 4,5 }
(ii) { a, b, c } . . . { b, c, d }
(iii) {x : x is a student of Class XI of your school}. . .{x : x student of your school}
(iv) {x : x is a circle in the plane} . . .{x : x is a circle in the same plane with radius 1 unit}
(v) {x : x is a triangle in a plane} . . . {x : x is a rectangle in the plane}
(vi) {x : x is an equilateral triangle in a plane} . . . {x : x is a triangle in the same plane}
(vii) {x : x is an even natural number} . . . {x : x is an integer}

Question 2. Examine whether the following statements are true or false:

(i) { a, b } { b, c, a }
(ii) { a, e } ⊂ { x : x is a vowel in the English alphabe t}
(iii) { 1, 2, 3 } ⊂ { 1, 3, 5 }
(iv) { a }⊂ { a, b, c }
(v) { a }∈ { a, b, c }
(vi) { x : x is an even natural number less than 6} ⊂ { x : x is a natural number which divides 36}

Question 3. Let A = { 1, 2, { 3, 4 }, 5 }. Which of the following statements are incorrect and why?

(i) {3, 4} ⊂ A
(ii) {3, 4} ∈ A
(iii) {{3, 4}} ⊂ A (iv) 1 ∈ A
(v) 1 ⊂ A
(vi) {1, 2, 5} ⊂ A
(vii) {1, 2, 5} ∈ A
(viii) {1, 2, 3} ⊂ A
(ix) φ ∈ A
(x) φ ⊂ A
(xi) {φ} ⊂ A

Question 4. Write down all the subsets of the following sets

(i) {a}
(ii) {a, b}
(iii) {1, 2, 3}
(iv) φ

Question 5. How many elements has P(A), if A = φ? 6. Write the following as intervals :

(i) {x : x ∈ R, – 4 < x ≤ 6}
(ii) {x : x ∈ R, – 12 < x < –10}
(iii) {x : x ∈ R, 0 ≤ x < 7}
(iv) {x : x ∈ R, 3 ≤ x ≤ 4}

Question 6. Write the following intervals in set-builder form :

(i) (– 3, 0)
(ii) [6 , 12]
(iii) (6, 12]
(iv) [–23, 5)

Question 7. What universal set(s) would you propose for each of the following :

(i) The set of right triangles.
(ii) The set of isosceles triangles.

Question 8. Given the sets A = {1, 3, 5}, B = {2, 4, 6} and C = {0, 2, 4, 6, 8}, which of the following may be considered as universal set (s) for all the three sets A, B and C

(i) {0, 1, 2, 3, 4, 5, 6}
(ii) φ
(iii) {0,1,2,3,4,5,6,7,8,9,10}
(iv) {1,2,3,4,5,6,7,8}

EXERCISE 1.4

Question 1. Find the union of each of the following pairs of sets :

(i) X = {1, 3, 5} Y = {1, 2, 3}
(ii) A = [ a, e, i, o, u} B = {a, b, c}
(iii) A = {x : x is a natural number and multiple of 3} B = {x : x is a natural number less than 6}
(iv) A = {x : x is a natural number and 1 < x ≤ 6 } B = {x : x is a natural number and 6 < x < 10 }
(v) A = {1, 2, 3}, B = φ

Question 2. Let A = { a, b }, B = {a, b, c}. Is A ⊂ B ? What is A ∪ B ?

Question 3. If A and B are two sets such that A ⊂ B, then what is A ∪ B ?

Question 4. If A = {1, 2, 3, 4}, B = {3, 4, 5, 6}, C = {5, 6, 7, 8 }and D = { 7, 8, 9, 10 }; find

(i) A ∪ B
(ii) A ∪ C
(iii) B ∪ C
(iv) B ∪ D
(v) A ∪ B ∪ C
(vi) A ∪ B ∪ D
(vii) B ∪ C ∪ D

Question 5. Find the intersection of each pair of sets of question 1 above.

Question 6. If A = { 3, 5, 7, 9, 11 }, B = {7, 9, 11, 13}, C = {11, 13, 15}and D = {15, 17}; find

(i) A ∩ B
(ii) B ∩ C
(iii) A ∩ C ∩ D
(iv) A ∩ C
(v) B ∩ D (vi) A ∩ (B ∪ C)
(vii) A ∩ D
(viii) A ∩ (B ∪ D)
(ix) ( A ∩ B ) ∩ ( B ∪ C ) (x) ( A ∪ D) ∩ ( B ∪ C)

Question 7. If A = {x : x is a natural number }, B = {x : x is an even natural number} C = {x : x is an odd natural number}andD = {x : x is a prime number }, find

(i) A ∩ B
(ii) A ∩ C
(iii) A ∩ D
(iv) B ∩ C
(v) B ∩ D
(vi) C ∩ D

Question 8. Which of the following pairs of sets are disjoint

(i) {1, 2, 3, 4} and {x : x is a natural number and 4 ≤ x ≤ 6 }
(ii) { a, e, i, o, u } and { c, d, e, f }
(iii) {x : x is an even integer } and {x : x is an odd integer} ]

Question 9. If A = {3, 6, 9, 12, 15, 18, 21}, B = { 4, 8, 12, 16, 20 }, C = { 2, 4, 6, 8, 10, 12, 14, 16 }, D = {5, 10, 15, 20 }; find

(i) A – B
(ii) A – C
(iii) A – D
(iv) B – A
(v) C – A
(vi) D – A
(vii) B – C
(viii) B – D
(ix) C – B
(x) D – B
(xi) C – D
(xii) D – C

Question 10. If X= { a, b, c, d } and Y = { f, b, d, g}, find

(i) X – Y
(ii) Y – X
(iii) X ∩ Y

Question 11. If R is the set of real numbers and Q is the set of rational numbers, then what is R – Q?

Question 12. State whether each of the following statement is true or false. Justify your answer.

(i) { 2, 3, 4, 5 } and { 3, 6} are disjoint sets.
(ii) { a, e, i, o, u } and { a, b, c, d }are disjoint sets.
(iii) { 2, 6, 10, 14 } and { 3, 7, 11, 15} are disjoint sets.
(iv) { 2, 6, 10 } and { 3, 7, 11} are disjoint sets.
 

EXERCISE 1.5

Question 1. Let U = { 1, 2, 3, 4, 5, 6, 7, 8, 9 }, A = { 1, 2, 3, 4}, B = { 2, 4, 6, 8 } and C = { 3, 4, 5, 6 }. Find

(i) A′
(ii) B′
(iii) (A ∪ C)′
(iv) (A ∪ B)′
(v) (A′)′
(vi) (B – C)′

Question 2. If U = { a, b, c, d, e, f, g, h}, find the complements of the following sets :

(i) A = {a, b, c}
(ii) B = {d, e, f, g}
(iii) C = {a, c, e, g} (iv) D = { f, g, h, a}

Question 3. Taking the set of natural numbers as the universal set, write down the complements of the following sets:

(i) {x : x is an even natural number}
(ii) { x : x is an odd natural number }
(iii) {x : x is a positive multiple of 3}
(iv) { x : x is a prime number }
(v) {x : x is a natural number divisible by 3 and 5}
(vi) { x : x is a perfect square }
(vii) { x : x is a perfect cube}
(viii) { x : x + 5 = 8 }
(ix) { x : 2x + 5 = 9} (x) { x : x ≥ 7 }
(xi) { x : x ∈ N and 2x + 1 > 10 }

Question 4. If U = {1, 2, 3, 4, 5, 6, 7, 8, 9 }, A = {2, 4, 6, 8} and B = { 2, 3, 5, 7}. Verify that

(i) (A ∪ B)′ = A′ ∩ B′
(ii) (A ∩ B)′ = A′ ∪ B′

Question 5. Draw appropriate Venn diagram for each of the following :

(i) (A ∪ B)′
(ii) A′ ∩ B′
(iii) (A ∩ B)′,
(iv) A′ ∪ B′

Question 6. Let U be the set of all triangles in a plane. If A is the set of all triangles with at least one angle different from 60°, what is A′?

Question 7. Fill in the blanks to make each of the following a true statement :

(i) A ∪ A′ = . . .
(ii) φ′ ∩ A = . . .
(iii) A ∩ A′ = . . .
(iv) U′ ∩ A = . . .

EXERCISE 1.6

Question 1. If X and Y are two sets such that n ( X ) = 17, n ( Y ) = 23 and n ( X ∪ Y ) = 38, find n ( X ∩ Y ).

Question 2. If X and Y are two sets such that X ∪ Y has 18 elements, X has 8 elements and Y has 15 elements ; how many elements does X ∩ Y have?

Question 3. In a group of 400 people, 250 can speak Hindi and 200 can speak English. How many people can speak both Hindi and English?

Question 4. If S and T are two sets such that S has 21 elements, T has 32 elements, and S ∩ T has 11 elements, how many elements does S ∪ T have?

Question 5. If X and Y are two sets such that X has 40 elements, X ∪ Y has 60 elements and X ∩ Y has 10 elements, how many elements does Y have?

Question 6. In a group of 70 people, 37 like coffee, 52 like tea and each person likes at least one of the two drinks. How many people like both coffee and tea?

Question 7. In a group of 65 people, 40 like cricket, 10 like both cricket and tennis. How many like tennis only and not cricket? How many like tennis?

Question 8. In a committee, 50 people speak French, 20 speak Spanish and 10 speak both Spanish and French. How many speak at least one of these two languages?

---

(Mathematics) : Chapter 2 Relations And Functions

---

EXERCISE  2.1

Qusetion 1. If 1 2 5 1 3 3 33 , find the values of x and y.

Question 2. If the set A has 3 elements and the set B = {3, 4, 5}, then find the number of elements in (A×B).

Question 3. If G = {7, 8} and H = {5, 4, 2}, find G × H and H × G.

Question 4. State whether each of the following statements are true or false. If the statement is false, rewrite the given statement correctly.

(i) If P = {m, n} and Q = { n, m}, then P × Q = {(m, n),(n, m)}.
(ii) If A and B are non-empty sets, then A × B is a non-empty set of ordered pairs (x, y) such that x ∈ A and y ∈ B.
(iii) If A = {1, 2}, B = {3, 4}, then A × (B ∩ φ) = φ.

Question 5. If A = {–1, 1}, find A × A × A. 6. If A × B = {(a, x),(a , y), (b, x), (b, y)}. Find A and B.

Question 6. Let A = {1, 2}, B = {1, 2, 3, 4}, C = {5, 6} and D = {5, 6, 7, 8}. Verify that (i) A × (B ∩ C) = (A × B) ∩ (A × C). (ii) A × C is a subset of B × D.

Question 7. Let A = {1, 2} and B = {3, 4}. Write A × B. How many subsets will A × B have? List them.

Question 8. Let A and B be two sets such that n(A) = 3 and n(B) = 2. If (x, 1), (y, 2), (z, 1) are in A × B, find A and B, where x, y and z are distinct elements.

Question 10. The Cartesian product A × A has 9 elements among which are found (–1, 0) and\ (0,1). Find the set A and the remaining elements of A × A

EXERCISE  2.2

Qusetion 1. Let A = {1, 2, 3,...,14}. Define a relation R from A to A by R = {(x, y) : 3x – y = 0, where x, y ∈ A}. Write down its domain, codomain and range. 

Question 2. Define a relation R on the set N of natural numbers by R = {(x, y) : y = x + 5, x is a natural number less than 4; x, y ∈N}. Depict this relationship using roster form. Write down the domain and the range.

Question 3. A = {1, 2, 3, 5} and B = {4, 6, 9}. Define a relation R from A to B by R = {(x, y): the difference between x and y is odd; x ∈ A, y ∈ B}. Write R in roster form.

Question 4. The Fi 2.7 shows a relationship between the sets P and Q. Write this relation (i) in set-builder form (ii) roster form. What is its domain and range?

Question 5. Let A = {1, 2, 3, 4, 6}. Let R be the relation on A defined by {(a, b): a , b ∈A, b is exactly divisible by a}.

(i) Write R in roster form
(ii) Find the domain of R
(iii) Find the range of R.

Question 6. Determine the domain and range of the relation R defined by R = {(x, x + 5) : x ∈ {0, 1, 2, 3, 4, 5}}.

Question 7. Write the relation R = {(x, x3) : x is a prime number less than 10} in roster form.

Question 8. Let A = {x, y, z} and B = {1, 2}. Find the number of relations from A to B.

Question 9. Let R be the relation on Z defined by R = {(a,b): a, b ∈ Z, a – b is an integer}. Find the domain and range of R.

EXERCISE 2.3

Qusetion 1. Which of the following relations are functions? Give reasons. If it is a function, determine its domain and range.

(i) {(2,1), (5,1), (8,1), (11,1), (14,1), (17,1)}
(ii) {(2,1), (4,2), (6,3), (8,4), (10,5), (12,6), (14,7)}
(iii) {(1,3), (1,5), (2,5)}.

Question 2. Find the domain and range of the following real functions: (i) f(x) = – x (ii) f(x) = 9 − x 2.

Question 3. A function f is defined by f(x) = 2x –5. Write down the values of (i) f (0), (ii) f (7), (iii) f (–3).

Question 4. The function ‘t’ which maps temperature in degree Celsius into temperature in degree Fahrenheit is defined by tC) = 9C 5 + 3 2.Find

(i) t(0)
(ii) t(28)
(iii) t(–10)
(iv) The value of C, when t(C) = 212.

Question 5. Find the range of each of the following functions.

(i) f (x) = 2 – 3x, x ∈ R, x > 0.
(ii) f (x) = x2 + 2, x is a real number.
(iii) f (x) = x, x is a real number 

---

(Mathematics) : Chapter 3 Trigonometric Functions

---

EXERCISE 3. 1

Question 1. Find the radian measures corresponding to the following degree measures:

(i) 25°
(ii) – 47°30
(iii)240°
(iv) 520°

Question 2. Find the degree measures corresponding to the following radian measurs (Use π 22 7 = ).

(i) 11 16
(ii) – 4
(iii) 5π 3
(iv) 7π 6

Question 3. A wheel makes 360 revolutions in one minute. Through how many radians does it turn in one second?

Question 4. Find the degree measure of the angle subtended at the centre of a circle of radius 100 cm by an arc of length 22 cm (Use π 22 7 = ).

Question 5. In a circle of diameter 40 cm, the length of a chord is 20 cm. Find the length of minor arc of the chord.

Question 6. If in two circles, arcs of the same length subtend angles 60° and 75° at the centre, find the ratio of their radii.

Question 7. Find the angle in radian through which a pendulum swings if its length is 75 cm and th e tip describes an arc of length (i) 10 cm (ii) 15 cm (iii) 21 cm

EXERCISE 3. 2

Find the values of other five trigonometric functions in Exercises 1 to 5.

Question 1. cos x = – 1 2 , x lies in third quadrant.

Question 2. sin x = 3 5, x lies in second quadrant.

Question 3. cot x = 4 3 , x lies in third quadrant.

Question 4. sec x = 13 5 , x lies in fourth quadrant.

Question 5. tan x = – 5 12 , x lies in second quadrant. Find the values of the trigonometric functions in Exercises 6 to 10.

Question 6. sin 765°

Question 7. cosec (– 1410°) 8. tan 19π 3 9. sin (– 11π 3 ) 10. cot (– 15π 4 )

EXERCISE  3. 3

Prove that:

Question 1. sin2 π 6 + cos2 3 π – tan2 – 1 4 2 π =

Question 2. 2sin2 6 π + cosec2 7 cos2 3 6 3 2 π π =

Question 3. cot2 cosec 5 3tan2 6 6 6 6 π π π + + =

Question 4. 2sin2 3 2cos2 2sec2 10 4 4 3 π π π + + =

Question 5. Find the value of:
(i) sin 75°
(ii) tan 15°

Find the principal and general solutions of the following equations:

Question 6. tan x = 3

Question 7. sec x = 2

Question 8. cot x = − 3

Question 9. cosec x = – 2

Find the general solution for each of the following equations:

Question 10. cos 4 x = cos 2 x

Question 11. cos 3x + cos x – cos 2x = 0

Question 12. sin 2x + cosx = 0 8. sec2 2x = 1– tan 2x

---

(Mathematics) : Chapter 4 Principle of Mathematical Induction 

---

EXERCISE 4.1

Prove the following by using the principle of mathematical induction for all n ∈ N:

Question 1. 1 + 3 + 32 + ... + 3n – 1 = (3 1) 2 n − .

Question 2. 13 + 23 + 33 + … +n3 = 2 ( 1) 2 n n + .

Question 3. 1 1 1 1 2 (1 2) (1 2 3) (1 2 3 ) ( 1) ... n ...n n + + + + = + + + + + + + .

Question 4. 1.2.3 + 2.3.4 +…+ n(n+1) (n+2) = ( 1)( 2)( 3) 4 n n + n + n + .

Question 5. 1.3 + 2.32 + 3.33 +…+ n.3n = (2 1)3 1 3 4 n − n+ + .

Question 6. 1.2 + 2.3 + 3.4 +…+ n.(n+1) = ( 1)( 2) 3 n n + n +.

Question 7. 1.3 + 3.5 + 57 +…+ (2n–1) (2n+1) = (4 2 6 1) 3 n n + n − .

Question 8. 1.2 + 2.22 + 3.22 + ...+n.2n = (n–1) 2n + 1 + 2.

Question 9. 1 1 1 ... 1 1 1 2 4 8 2n 2n + + + + = − .

Question 10. 1 1 1 ... 1 2.5 5.8 8.11 (3 1)(3 2) (6 4) n n n n + + + + = − + + .

Question 11. 1 1 1 ... 1 ( 3) 1.2.3 2.3.4 3.4.5 ( 1)( 2) 4( 1)( 2)

Question 12. a + ar + ar2 +…+ arn-1 = ( 1) 1 a rn r − − .

Question 13. 2 2 1 3 1 5 1 7 ... 1 (2 1) ( 1) 1 4 9 n n

Question 14. 12 + 32 + 52 + …+ (2n–1)2 = (2 1)(2 1) 3 n n − n + .

Question 15. 1 1 1 ... 1 1.4 4.7 7.10 (3 2)(3 1) (3 1) n n n n + + + + = − + + .

Question 16. 1 1 1 ... 1 3.5 5.7 7.9 (2 1)(2 3) 3(2 3) n n n n + + + + = + + + .

Question 17. 1 + 2 + 3 +…+ n < 1 8 (2n + 1)2.

Question 18. n (n + 1) (n + 5) is a multiple of 3.

Question 19. 102n – 1 + 1 is divisible by 11.

Question 20. x2n – y2n is divisible by x + y.

Question 21. 32n+2 – 8n – 9 is divisible by 8.

Question 22. 41n – 14n is a multiple of 27.

Question 23."> (2n + 7) < (n + 3)2.

---

(Mathematics) : Chapter 5 Complex Numbers and Quadratic Equations

---

EXERCISE 5.1

Question 1. z = – 1 – i

Question 2. z = – + i Convert each of the complex numbers given in Exercises 3 to 8 in the polar form:

Question 3. 1 – i 4. – 1 + i 5. – 1 – i 6. – 3 7. + i 8. i

EXERCISE 5.2

Solve each of the following equations:

Question 1. x2 + 3 = 0

Question 2. 2x2 + x + 1 = 0

Question 3. x2 + 3x + 9 = 0

Question 4. – x2 + x – 2 = 0

Question 5. x2 + 3x + 5 = 0

Question 6. x2 – x + 2 = 0

Question 7. 2x2 + x + 2 = 0

Question 8. 3x2 − 2x + 3 3 = 0

Question 9. 2 1 0 2 x + x + =

Question 10. 2 1 0 2 x + x

---

(Mathematics) : Chapter 6 Linear Inequalities

---

EXERCISE 6.1

Question 1. Solve 24x < 100, when
(i) x is a natural number.
(ii) x is an integer.

Question 2.Solve – 12x > 30, when
(i) x is a natural number.
(ii) x is an integer.

Question 3. Solve 5x – 3 < 7, when
(i) x is an integer.
(ii) x is a real number.

Question 4. Solve 3x + 8 >2, when
(i) x is an integer.
(ii) x is a real number. Solve the inequalities in Exercises 5 to 16 for real x.

Question 5. 4x + 3 < 6x + 7

Question 6. 3x – 7 > 5x – 1

Question 7. 3(x – 1) ≤ 2 (x – 3)

Question 8.3 (2 – x) ≥ 2 (1 – x)

Question 9. 11 2 3 x + x + x <

Question 10. 1 3 2 x x > +

Question 11. 3( 2) 5(2 ) 5 3 x − − x ≤

Question 12. 1 3 4 1 ( 6) 2 5 3 x + ⎞≥ x −

Question 13. 2 (2x + 3) – 10 < 6 (x – 2)

Question 14. 37 – (3x + 5) > 9x – 8 (x – 3)

Question 15. (5 2) (7 3) 4 3 5 x x− x − < −

Question 16. (2 1) (3 2) (2 ) 3 4 5 x − x − − x ≥ −

Solve the inequalities in Exercises 17 to 20 and show the graph of the solution in each case on number line

Question 17. 3x – 2 < 2x + 1

Question 18. 5x – 3 > 3x – 5

Question 19. 3 (1 – x) < 2 (x + 4)

Question 20. (5 2) (7 3) 2 3 5 x x − x − < −

Question 21. Ravi obtained 70 and 75 marks in first two unit test. Find the number if minimum marks he should get in the third test to have an average of at least 60 marks.

Question 22. To receive Grade ‘A’ in a course, one must obtain an average of 90 marks or more in five examinations (each of 100 marks). If Sunita’s marks in first four examinations are 87, 92, 94 and 95, find minimum marks that Sunita must obtain in fifth examination to get grade ‘A’ in the course.

Question 23. Find all pairs of consecutive odd positive integers both of which are smaller than 10 such that their sum is more than 11.

Question 24. Find all pairs of consecutive even positive integers, both of which are larger than 5 such that their sum is less than 23.

Question 25. The longest side of a triangle is 3 times the shortest side and the third side is 2 cm shorter than the longest side. If the perimeter of the triangle is at least 61 cm, find the minimum length of the shortest side.

Question 26. A man wants to cut three lengths from a single piece of board of length 91cm. The second length is to be 3cm longer than the shortest and the third length is to be twice as long as the shortest. What are the possible lengths of the shortest board if the third piece is to be at least 5cm longer than the second? [Hint: If x is the length of the shortest board, then x , (x + 3) and 2x are the lengths of the second and third piece, respectively. Thus, x + (x + 3) + 2x ≤ 91 and 2x ≥ (x + 3) + 5]

---

(Mathematics) : Chapter 7 Permutations And Combinations

---

EXERCISE 7.1

Question 1.How many 3-digit numbers can be formed from the digits 1, 2, 3, 4 and 5 assuming that
(i) repetition of the digits is allowed?
(ii) repetition of the digits is not allowed?

Question 2.How many 3-digit even numbers can be formed from the digits 1, 2, 3, 4, 5, 6 if the digits can be repeated?

Question 3.How many 4-letter code can be formed using the first 10 letters of the English alphabet, if no letter can be repeated?

Question 4.How many 5-digit telephone numbers can be constructed using the digits 0 to 9 if each number starts with 67 and no digit appears more than once?

Question 5.A coin is tossed 3 times and the outcomes are recorded. How many possible outcomes are there?

Question 6.Given 5 flags of different colours, how many different signals can be generated if each signal requires the use of 2 flags, one below the other?

EXERCISE 7.2

Question 1.Evaluate
(i) 8 !
(ii) 4 ! – 3 !

Question 2.Is 3 ! + 4 ! = 7 ! ?

Question 3.Compute 8! 6!× 2!

Question 4.If 1 1 6! 7! 8! + = x , find x

Question 5.Evaluate ( ) ! ! n n − r , when
(i) n = 6, r = 2
(ii) n = 9, r = 5.

EXERCISE 7.3

Question 1.How many 3-digit numbers can be formed by using the digits 1 to 9 if no digit is repeated?

Question 2.How many 4-digit numbers are there with no digit repeated?

Question 3.How many 3-digit even numbers can be made using the digits 1, 2, 3, 4, 6, 7, if no digit is repeated?

Question 4.Find the number of 4-digit numbers that can be formed using the digits 1, 2, 3, 4, 5 if no digit is repeated. How many of these will be even?

Question 5.From a committee of 8 persons, in how many ways can we choose a chairman and a vice chairman assuming one person can not hold more than one position?

Question 6.Find n if n – 1P3 : nP4 = 1 : 9.

Question 7.Find r if
(i) 5 6 Pr 2 Pr−1 =
(ii) 5 6 Pr Pr−1 = .

Question 8.How many words, with or without meaning, can be formed using all the letters of the word EQUATION, using each letter exactly once?

Question 9.How many words, with or without meaning can be made from the letters of the word MONDAY, assuming that no letter is repeated, if. (i) 4 letters are used at a time, (ii) all letters are used at a time, (iii) all letters are used but first letter is a vowel?

Question 10.In how many of the distinct permutations of the letters in MISSISSIPPI do the four I’s not come together?

Question 11.In how many ways can the letters of the word PERMUTATIONS be arranged if the (i) words start with P and end with S, (ii) vowels are all together, (iii) there are always 4 letters between P and S?

EXERCISE 7.4

Question 1.If nC8 = nC2, find nC 2.

Question 2.Determine n if (i) 2nC2 : nC2 = 12 : 1 (ii) 2nC3 : nC3 = 11 : 1

Question 3.How many chords can be drawn through 21 points on a circle?

Question 4.In how many ways can a team of 3 boys and 3 girls be selected from 5 boys and 4 girls?

Question 5.Find the number of ways of selecting 9 balls from 6 red balls, 5 white balls and 5 blue balls if each selection consists of 3 balls of each colour.

Question 6.Determine the number of 5 card combinations out of a deck of 52 cards if there is exactly one ace in each combination.

Question 7.In how many ways can one select a cricket team of eleven from 17 players in which only 5 players can bowl if each cricket team of 11 must include exactly 4 bowlers?

Question 8.A bag contains 5 black and 6 red balls. Determine the number of ways in which 2 black and 3 red balls can be selected.

Question 9.In how many ways can a student choose a programme of 5 courses if 9 courses are available and 2 specific courses are compulsory for every student?

---

(Mathematics) :  Chapter 8 Binomial Theorem

---

EXERCISE 8.1

Expand each of the expressions in Exercises 1 to 5. Using binomial theorem, evaluate each of the following:

 

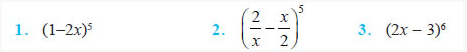
Question 6. (96)3

Question 7. (102)5

Question 8. (101)4

Question 9. (99)5

Question 10. Using Binomial Theorem, indicate which number is larger (1.1)10000 or 1000.

Question 11. Find (a + b)4 – (a – b)4. Hence, evaluate ( 3 + 2)4– ( 3 – 2)4 .

Question 12. Find (x + 1)6 + (x – 1)6. Hence or otherwise evaluate ( 2 + 1)6 + ( 2 – 1)6.

Question 13. Show that 9n+1 – 8n – 9 is divisible by 64, whenever n is a positive integer.

EXERCISE 8.2

Find the coefficient of

Question 1. x5 in (x + 3)8 2. a5b7 in (a – 2b)1

Question 2. Write the general term in the expansion of

Question 3. (x2 – y)6

Question 4. (x2 – yx)12, x ≠ 0.

Question 5. Find the 4th term in the expansion of (x – 2y)12.

Question 6. Find the 13th term in the expansion of 18 9 1 3 x x , x ≠ 0. Find the middle terms in the expansions of

Question 7. 3 7 6 3 − x

Question 8. 10 9 3 x + y

Question 9. In the expansion of (1 + a)m+n, prove that coefficients of am and an are equal.

Question 10. The coefficients of the (r – 1)th, rth and (r + 1)th terms in the expansion of (x + 1)n are in the ratio 1 : 3 : 5. Find n and r.

Question 11. Prove that the coefficient of xn in the expansion of (1 + x)2n is twice the coefficient of xn in the expansion of (1 + x)2n – 1.

Question 12. Find a positive value of m for which the coefficient of x2 in the expansion (1 + x)m is 6.

 

Click Here to Download Full Paper

---

(Mathematics) : Chapter 9 Sequences and Series

---

EXERCISE 9.1

Write the first five terms of each of the sequences in Exercises 1 to 6 whose nth terms are:

Question 1.an = n (n + 2)

Question 2.an = 1 n n +

Question 3.an = 2n

Question 4.an = 2 3 6 n −

Question 5.an = (–1)n–1 5n+1

Question 6.an 2 5 4 n n + = . Find the indicated terms in each of the sequences in Exercises 7 to 10 whose nth terms are:

Question 7.an = 4n – 3; a17, a24

Question 8.an = 2 7 ; 2n n a

Question 9.an = (–1)n – 1n3; a9 Write the first five terms of each of the sequences in Exercises 11 to 13 and obtain the corresponding series:

Question 10.20 ( –2); n 3 a n n a n =

EXERCISE 9.2

Question 1.Find the sum of odd integers from 1 to 2001.

Question 2.Find the sum of all natural numbers lying between 100 and 1000, which are multiples of 5.

Question 3.In an A.P., the first term is 2 and the sum of the first five terms is one-fourth of the next five terms. Show that 20th term is –11 2.

Question 4.How many terms of the A.P. – 6, 11 2 − , – 5, … are needed to give the sum –25?

Question 5.In an A.P., if pth term is 1 q and qth term is 1 p , prove that the sum of first pq terms is 1 2 (pq +1), where p ≠ q.

Question 6.If the sum of a certain number of terms of the A.P. 25, 22, 19, … is 11 7 Find the last term. Find the sum to n terms of the A.P., whose kth term is 5k +1

Question 8.If the sum of n terms of an A.P. is (pn + qn2), where p and q are constants, find the common difference.

Question 9.The sums of n terms of two arithmetic progressions are in the ratio 5n + 4 : 9n + 6. Find the ratio of their 18th terms.

Question 10.If the sum of first p terms of an A.P. is equal to the sum of the first q terms, then find the sum of the first (p + q) terms. 1

Question 11.Sum of the first p, q and r terms of an A.P are. a, b and c, respectively. Prove that a (q r) b (r p) c ( p q) 0 p q r − + − + − = 1

Question 12.The ratio of the sums of m and n terms of an A.P. is m2 : n 2.Show that the ratio of mth and nth term is (2m – 1) : (2n – 1). 1

Question 13.If the sum of n terms of an A.P. is 3n2 + 5n and its mth term is 164, find the value of m. 1

Question 14.Insert five numbers between 8 and 26 such that the resulting sequence is an A.P. 1

Question 15.If 1 1 n n n n a b a − b − + + is the A.M. between a and b, then find the value of n.

Question 16.Between 1 and 31, m numbers have been inserted in such a way that the resulting sequence is an A. P. and the ratio of 7th and (m – 1)th numbers is 5 9. Find the value of m.

Question 17.A man starts repaying a loan as first instalment of Rs. 100. If he increases the instalment by Rs 5 every month, what amount he will pay in the 30th instalment?

Question 18.The difference between any two consecutive interior angles of a polygon is 5°. If the smallest angle is 120° , find the number of the sides of the polygon.

EXERCISE 9.3

Question 1.Find the 20th and nth terms of the G.P. 5 5 5 2 4 8 , , , ...

Question 2.Find the 12th term of a G.P. whose 8th term is 192 and the common ratio is 2.

Question 3.The 5th, 8th and 11th terms of a G.P. are p, q and s, respectively. Show that q2 = ps.

Question 4.The 4th term of a G.P. is square of its second term, and the first term is – 3. Determine its 7th term.

Question 5.Which term of the following sequences: (a) 2,2 2,4,... is 128 ? (b) 3,3,3 3,...is729 ? (c) 1 1 1 is 1 3 9 27 19683 , , ,... ?

Question 6.For what values of x, the numbers 2 2 7 7 – ,x,– are in G.P.? Find the sum to indicated number of terms in each of the geometric progressions in Exercises 7 to 10:

Question 7.0.15, 0.015, 0.0015, ... 20 terms.

Question 8.7 , 21 , 3 7 , ... n terms.

Question 9.1, – a, a2, – a3, ... n terms (if a ≠ – 1).

Question 10.x3, x5, x7, ... n terms (if x ≠ ± 1).

Question 11.Evaluate 11 1 (2 3k ) k = Σ + . 1

Question 12.The sum of first three terms of a G.P. is 39 10 and their product is 1. Find the common ratio and the terms.

Question 13.How many terms of G.P. 3, 32, 33, … are needed to give the sum 120?

Question 14.The sum of first three terms of a G.P. is 16 and the sum of the next three terms is 12 8. Determine the first term, the common ratio and the sum to n terms of the G.P.

Question 15.Given a G.P. with a = 729 and 7th term 64, determine S 7.

Question 16.Find a G.P. for which sum of the first two terms is – 4 and the fifth term is 4 times the third term.

Question 17.If the 4th, 10th and 16th terms of a G.P. are x, y and z, respectively. Prove that x, y, z are in G.P.

Question 18.Find the sum to n terms of the sequence, 8, 88, 888, 8888… .

Question 19.Find the sum of the products of the corresponding terms of the sequences 2, 4, 8, 16, 32 and 128, 32, 8, 2, 1 2 20.

Show that the products of the corresponding terms of the sequences a, ar, ar2, …arn – 1 and A, AR, AR2, … ARn – 1 form a G.P, and find the common ratio.

Question 1.Find four numbers forming a geometric progression in which the third term is greater than the first term by 9, and the second term is greater than the 4th by 18.

Question 2.If the pth, qth and rth terms of a G.P. are a, b and c, respectively. Prove that aq – r br – pcP – q =1.

Question 3.If the first and the nth term of a G.P. are a and b, respectively, and if P is the product of n terms, prove that P2 = (ab)n.

Question 4.Show that the ratio of the sum of first n terms of a G.P. to the sum of terms from (n + 1)th to (2n)th term is 1 rn .

Question 5.If a, b, c and d are in G.P. show that (a2 + b2 + c2) (b2 + c2 + d2) = (ab + bc + cd)2

Question 6.Insert two number between 3 and 81 so that the resulting sequence is G.P. 2

Question 7.Find the value of n so that a b a b n n n n + + + + 1 1 may be the geometric mean between a and b.

Question 8.The sum of two numbers is 6 times their geometric means, show that numbers are in the ratio (3+ 2 2 ): (3−2 2).

Question 9.If A and G be A.M. and G.M., respectively between two positive numbers, prove that the numbers are A A G A G ( )( ) ± + −. 30.

The number of bacteria in a certain culture doubles every hour. If there were 30 bacteria present in the culture originally, how many bacteria will be present at the end of 2nd hour, 4th hour and nth hour ?

Question 1.What will Rs 500 amounts to in 10 years after its deposit in a bank which pays annual interest rate of 10% compounded annually?

Question 2.If A.M. and G.M. of roots of a quadratic equation are 8 and 5, respectively, then obtain the quadratic equation

EXERCISE 9.4

Find the sum to n terms of each of the series in Exercises 1 to 7.

Question 1. 1 × 2 + 2 × 3 + 3 × 4 + 4 × 5 +...

Question 2. 1 × 2 × 3 + 2 × 3 × 4 + 3 × 4 × 5 + ...

Question 3. 3 × 12 + 5 × 22 + 7 × 32 + ...

Question 4. 1 1 1 1 2 2 3 3 4 + + + × × × ...

Question 5. 52 + 62 + 72 + ... + 202

Question 6 .3 × 8 + 6 × 11 + 9 × 14 + ...

Question 7. 12 + (12 + 22) + (12 + 22 + 32) + ...

Find the sum to n terms of the series in Exercises 8 to 10 whose nth terms is given by

Question 8.n (n+1) (n+4).

Question 9.n2 + 2n

Question nbsp;10.(2n – 1)2

Miscellaneous Exercise On Chapter 9

Question 1.Show that the sum of (m + n)th and (m – n)th terms of an A.P. is equal to twice the mth term.

Question 2.If the sum of three numbers in A.P., is 24 and their product is 440, find the numbers.

Question 3.Let the sum of n, 2n, 3n terms of an A.P. be S1, S2 and S3, respectively, show that S3 = 3(S2 – S1)

Question 4.Find the sum of all numbers between 200 and 400 which are divisible by 7.

Question 5.Find the sum of integers from 1 to 100 that are divisible by 2 or 5.

Question 6.Find the sum of all two digit numbers which when divided by 4, yields 1 as remainder.

Question 7.If f is a function satisfying f (x +y) = f(x) f(y) for all x, y ∈ N such that f(1) = 3 and 1 ( ) 120 n x f x = Σ = , find the value of n.

Question 8.The sum of some terms of G.P. is 315 whose first term and the common ratio are 5 and 2, respectively. Find the last term and the number of terms

Question 9.The first term of a G.P. is 1. The sum of the third term and fifth term is 90. Find the common ratio of G.P.

Question 10.The sum of three numbers in G.P. is 5 6.If we subtract 1, 7, 21 from these numbers in that order, we obtain an arithmetic progression.

Find the numbers.

Question 1.A G.P. consists of an even number of terms. If the sum of all the terms is 5 times the sum of terms occupying odd places, then find its common ratio.

Question 2.The sum of the first four terms of an A.P. is 56.The sum of the last four terms is 12. If its first term is 11, then find the number of terms.

Question 3.If a bx a bx b cx b cx c dx c dx x + − = + − = + − ( ≠ 0) , then show that a, b, c and d are in G.P.

Question 4. Let S be the sum, P the product and R the sum of reciprocals of n terms in a G.P. Prove that P2Rn = Sn.

Question 5.The pth, qth and rth terms of an A.P. are a, b, c, respectively. Show that (q – r )a + (r – p )b + (p – q )c = 0

Question 6.If a 1 1 ,b 1 1 ,c 1 1 b c c a a b are in A.P., prove that a, b, c are in A.P.

Question 7.If a, b, c, d are in G.P, prove that (an + bn), (bn + cn), (cn + dn) are in G.P.

Question 8.If a and b are the roots of x2 – 3x + p = 0 and c, d are roots of x2 – 12x + q = 0, where a, b, c, d form a G.P. Prove that (q + p) : (q – p) = 17:15.

Question 9.The ratio of the A.M. and G.M. of two positive numbers a and b, is m : n. Show that a :b = (m + m2 – n2 ): (m – m2 – n2 ) 20. If a, b, c are in A.P.; b, c, d are in G.P. and 1 , 1 ,1 c d e are in A.P. prove that a, c, e are in G.P.

Question 10.Find the sum of the following series up to n terms: (i) 5 + 55 +555 + … (ii) .6 +. 66 +. 666+…

Question 11.Find the 20th term of the series 2 × 4 + 4 × 6 + 6 × 8 + ... + n terms.

Question 12.Find the sum of the first n terms of the series: 3+ 7 +13 +21 +31 +…

Question 13.If S1, S2, S3 are the sum of first n natural numbers, their squares and their cubes, respectively, show that 9 22 S = S3 (1 + 8S1).

Question 14 .Find the sum of the following series up to n terms: 13 13 22 13 23 33 1 1 3 1 3 5... + + + + + + + + +

Question 15.Show that 2 2 2 2 2 2 1 2 2 3 ( 1) 3 5 1 2 2 3 ( 1) 3 1 ... n n n ... n n n × + × + + × + + = × + × + + × + + .

Question 16.A farmer buys a used tractor for Rs 12000. He pays Rs 6000 cash and agrees to pay the balance in annual instalments of Rs 500 plus 12% interest on the unpaid amount. How much will the tractor cost him?

Question 17.Shamshad Ali buys a scooter for Rs 22000. He pays Rs 4000 cash and agrees to pay the balance in annual instalment of Rs 1000 plus 10% interest on the unpaid amount. How much will the scooter cost him?

Question 18.A person writes a letter to four of his friends. He asks each one of them to copy the letter and mail to four different persons with instruction that they move the chain similarly. Assuming that the chain is not broken and that it costs 50 paise to mail one letter. Find the amount spent on the postage when 8th set of letter is mailed.

---

(Mathematics) : Chapter 10 Straight Lines

---

EXERCISE 10.1

Question 1. Draw a quadrilateral in the Cartesian plane, whose vertices are (– 4, 5), (0, 7), (5, – 5) and (– 4, –2). Also, find its area.

Question 2. The base of an equilateral triangle with side 2a lies along the y-axis such that the mid-point of the base is at the origin. Find vertices of the triangle.

Question 3. Find the distance between P (x1, y1) and Q (x2, y2) when : (i) PQ is parallel to the y-axis, (ii) PQ is parallel to the x-axis.

Question 4. Find a point on the x-axis, which is equidistant from the points (7, 6) and (3, 4).

Question 5. Find the slope of a line, which passes through the origin, and the mid-point of the line segment joining the points P (0, – 4) and B (8, 0).

Question 6. Without using the Pythagoras theorem, show that the points (4, 4), (3, 5) and (–1, –1) are the vertices of a right angled triangle.

Question 7. Find the slope of the line, which makes an angle of 30° with the positive direction of y-axis measured anticlockwise.

Question 8. Find the value of x for which the points (x, – 1), (2,1) and (4, 5) are collinear.

Question 9. Without using distance formula, show that points (– 2, – 1), (4, 0), (3, 3) and (–3, 2) are the vertices of a parallelogram.

Question 10. Find the angle between the x-axis and the line joining the points (3,–1) and (4,–2).

Question 11. The slope of a line is double of the slope of another line. If tangent of the angle between them is 3 1 , find the slopes of the lines.

Question 12. A line passes through (x1, y1) and (h, k). If slope of the line is m, show that k – y1 = m (h – x1).

Question 13. If three points (h, 0), (a, b) and (0, k) lie on a line, show that + = 1 k b h a .

Question 14. Consider the following population and year graph (Fig 10.10), find the slope of the line AB and using it, find what will be the population in the year 2010?

EXERCISE 10.2

In Exercises 1 to 8, find the equation of the line which satisfy the given conditions:

Question 1. Write the equations for the x-and y-axes.

Question 2. Passing through the point (– 4, 3) with slope 2 1 .

Question 3. Passing through (0, 0) with slope m.

Question 4. Passing through (2, 2 3)and inclined with the x-axis at an angle of 75o.

Question 5. Intersecting the x-axis at a distance of 3 units to the left of origin with slope –2.

Question 6. Intersecting the y-axis at a distance of 2 units above the origin and making an angle of 30o with positive direction of the x-axis.

Question 7. Passing through the points (–1, 1) and (2, – 4).

Question 8. Perpendicular distance from the origin is 5 units and the angle made by the perpendicular with the positive x-axis is 300.

Question 9. The vertices of Δ PQR are P (2, 1), Q (–2, 3) and R (4, 5). Find equation of the median through the vertex R.

Question 10. Find the equation of the line passing through (–3, 5) and perpendicular to the line through the points (2, 5) and (–3, 6).

Question 11. A line perpendicular to the line segment joining the points (1, 0) and (2, 3) divides it in the ratio 1: n. Find the equation of the line.

Question 12. Find the equation of a line that cuts off equal intercepts on the coordinate axes and passes through the point (2, 3).

Question 13. Find equation of the line passing through the point (2, 2) and cutting off intercepts on the axes whose sum is 9.

Question 14. Find equation of the line through the point (0, 2) making an angle 2π 3 with the positive x-axis. Also, find the equation of line parallel to it and crossing the y-axis at a distance of 2 units below the origin.

Question 15. The perpendicular from the origin to a line meets it at the point (–2, 9), find the equation of the line.

Question 16. The length L (in centimetrs) of a copper rod is a linear function of its Celsius temperature C. In an experiment, if L = 124.942 when C = 20 and L= 125.134 when C = 110, express L in terms of C.

Question 17. The owner of a milk store finds that, he can sell 980 litres of milk each week at Rs 14/litre and 1220 litres of milk each week at Rs 16/litre. Assuming a linear relationship between selling price and demand, how many litres could he sell weekly at Rs 17/litre?

Question 18. P (a, b) is the mid-point of a line segment between axes. Show that equation of the line is + = 2 b y a x .

Question 19. Point R (h, k) divides a line segment between the axes in the ratio 1: 2. Find equation of the line.

Question 20. By using the concept of equation of a line, prove that the three points (3, 0), (– 2, – 2) and (8, 2) are collinear

EXERCISE 10.3

Question 1. Reduce the following equations into slope - intercept form and find their slopes and the y - intercepts.
(i) x + 7y = 0, (ii) 6x + 3y – 5 = 0, (iii) y = 0.

Question 2. Reduce the following equations into intercept form and find their intercepts on the axes.
(i) 3x + 2y – 12 = 0, (ii) 4x – 3y = 6, (iii) 3y + 2 = 0.

Question 3. Reduce the following equations into normal form. Find their perpendicular distances from the origin and angle between perpendicular and the positive x-axis. (i) x – 3y + 8 = 0, (ii) y – 2 = 0, (iii) x – y = 4.

Question 4. Find the distance of the point (–1, 1) from the line 12(x + 6) = 5(y – 2).

Question 5. Find the points on the x-axis, whose distances from the line 1 3 4 x y + = are 4 units.

Question 6. Find the distance between parallel lines
(i) 15x + 8y – 34 = 0 and 15x + 8y + 31 = 0 (ii) l (x + y) + p = 0 and l (x + y) – r = 0.

Question 7. Find equation of the line parallel to the line 3x − 4y + 2 = 0 and passing through the point (–2, 3).

Question 8. Find equation of the line perpendicular to the line x – 7y + 5 = 0 and having x intercept 3.

Question 9. Find angles between the lines 3x + y = 1and x + 3y = 1.

Question 10. The line through the points (h, 3) and (4, 1) intersects the line 7x − 9y −19 = 0. at right angle. Find the value of h .

Question 11. Prove that the line through the point (x1, y1) and parallel to the line Ax + By + C = 0 is A (x –x1) + B (y – y1) = 0.

Question 12. Two lines passing through the point (2, 3) intersects each other at an angle of 60o. If slope of one line is 2, find equation of the other line.

Question 13. Find the equation of the right bisector of the line segment joining the points (3, 4) and (–1, 2).

Question 14. Find the coordinates of the foot of perpendicular from the point (–1, 3) to the line 3x – 4y – 16 = 0.

Question 15. The perpendicular from the origin to the line y = mx + c meets it at the point (–1, 2). Find the values of m and c.

Question 16. If p and q are the lengths of perpendiculars from the origin to the lines x cosθ − ysin θ = k cos2θ and x sec θ + y cosec θ = k, respectively, prove that p2 + 4q2 = k2.

Question 17. In the triangle ABC with vertices A (2, 3), B (4, –1) and C (1, 2), find the equation and length of altitude from the vertex A.

Question 18. If p is the length of perpendicular from the origin to the line whose intercepts on the axes are a and b, then show that .

Miscellaneous Exercise on Chapter 10

Question 1. Find the values of k for which the line (k–3) x – (4 – k2) y + k2 –7k + 6 = 0 is (a) Parallel to the x-axis, (b) Parallel to the y-axis, (c) Passing through the origin.

Question 2. Find the values of θ and p, if the equation x cos θ + y sinθ = p is the normal form of the line 3 x + y + 2 = 0.

Question 3. Find the equations of the lines, which cut-off intercepts on the axes whose sum and product are 1 and – 6, respectively.

Question 4. What are the points on the y-axis whose distance from the line 1 3 4 x + y = is 4 units.

Question 5. Find perpendicular distance from the origin of the line joining the points (cosθ, sin θ) and (cos φ, sin φ).

Question 6. Find the equation of the line parallel to y-axis and drawn through the point of intersection of the lines x – 7y + 5 = 0 and 3x + y = 0.

Question 7. Find the equation of a line drawn perpendicular to the line 1 4 6 x + y = through the point, where it meets the y-axis.

Question 8. Find the area of the triangle formed by the lines y – x = 0, x + y = 0 and x – k = 0.

Question 9. Find the value of p so that the three lines 3x + y – 2 = 0, px + 2 y – 3 = 0 and 2x – y – 3 = 0 may intersect at one point.

Question 10. If three lines whose equations are y = m1x + c1, y = m2x + c2 and y = m3x + c3 are concurrent, then show that m1(c2 – c3) + m2 (c3 – c1) + m3 (c1 – c2) = 0

Question 11. Find the equation of the lines through the point (3, 2) which make an angle of 45o with the line x – 2y = 3.

Question 12. Find the equation of the line passing through the point of intersection of the lines 4x + 7y – 3 = 0 and 2x – 3y + 1 = 0 that has equal intercepts on the axes.

Question 13. Show that the equation of the line passing through the origin and making an angle θ with the line tan θ 1 tanθ y mx c is y m x m + = + = ±− .

Question 14. In what ratio, the line joining (–1, 1) and (5, 7) is divided by the line x + y = 4?

Question 15. Find the distance of the line 4x + 7y + 5 = 0 from the point (1, 2) along the line 2x – y = 0.

Question 16. Find the direction in which a straight line must be drawn through the point (–1, 2) so that its point of intersection with the line x + y = 4 may be at a distance of 3 units from this point.

Question 17. The hypotenuse of a right angled triangle has its ends at the points (1, 3) and (– 4, 1). Find the equation of the legs (perpendicular sides) of the triangle.

Question 18. Find the image of the point (3, 8) with respect to the line x +3y = 7 assuming the line to be a plane mirror.

Question 19. If the lines y = 3x +1 and 2y = x + 3 are equally inclined to the line y = mx + 4, find the value of m.

Question 20. If sum of the perpendicular distances of a variable point P (x, y) from the lines x + y – 5 = 0 and 3x – 2y +7 = 0 is always 10. Show that P must move on a line.

Question 21. Find equation of the line which is equidistant from parallel lines 9x + 6y – 7 = 0 and 3x + 2y + 6 = 0.

Question 22. A ray of light passing through the point (1, 2) reflects on the x-axis at point A and the reflected ray passes through the point (5, 3). Find the coordinates of A.

Question 23. Prove that the product of the lengths of the perpendiculars drawn from the points ( a2 − b2 ,0)and (− a2 − b2 ,0)to the line x cosθ y sin θ 1is b2 a b + = .

Question 24. A person standing at the junction (crossing) of two straight paths represented by the equations 2x – 3y + 4 = 0 and 3x + 4y – 5 = 0 wants to reach the path whose equation is 6x – 7y + 8 = 0 in the least time. Find equation of the path that he should follow.

---

(Mathematics) : Chapter 11 Conic Sections

---

EXERCISE 11.1

In each of the following Exercises 1 to 5, find the equation of the circle with

Question 1.centre (0,2) and radius2.

Question 2.centre (–2,3) and radius 4

Question 3.centre ( 4 , 1 2 1 ) and radius 12 1

Question 4.centre (1,1) and radius 2

Question 5.centre (–a, –b) and radius a2 − b 2.In each of the following Exercises 6 to 9, find the centre and radius of the circles.

Question 6.(x + 5)2 + (y – 3)2 = 36

Question 7.x2 + y2 – 4x – 8y – 45 = 0

Question 8.x2 + y2 – 8x + 10y – 12 = 0

Question 9.2x2 + 2y2 – x = 0

Question 10.Find the equation of the circle passing through the points (4,1) and (6,5) and whose centre is on the line 4x + y = 16.

Question 11.Find the equation of the circle passing through the points (2,3) and (–1,1) and whose centre is on the line x – 3y – 11 = 0.

Question 12.Find the equation of the circle with radius 5 whose centre lies on x-axis and passes through the point (2,3).

Question 13.Find the equation of the circle passing through (0,0) and making intercepts a and b on the coordinate axes.

Question 14.Find the equation of a circle with centre (2,2) and passes through the point (4,5).

Question1 5.Does the point (–2.5, 3.5) lie inside, outside or on the circle x2 + y2 = 25?

EXERCISE 11.2

In each of the following Exercises 1 to 6, find the coordinates of the focus, axis of the parabola, the equation of the directrix and the length of the latus rectum.

Question 1.y2 = 12x

Question 2.x2 = 6y

Question 3.y2 = – 8x

Question 4.x2 = – 16y

Question 5.y2 = 10x

Question 6.x2 = – 9y In each of the Exercises 7 to 12, find the equation of the parabola that satisfies the given conditions:

Question 7.Focus (6,0); directrix x = – 6

Question 8.Focus (0,–3); directrix y = 3

Question 9.Vertex (0,0); focus (3,0)

Question 10.Vertex (0,0); focus (–2,0 )

Question 1.Vertex (0,0) passing through (2,3) and axis is along x-axis.

Question 2.Vertex (0,0), passing through (5,2) and symmetric with respect to y-axis.

EXERCISE 11.3

In each of the Exercises 1 to 9, find the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of the latus rectum of the ellipse.

Question 1. 2 2 1 36 16 x + y =

Question 2. 2 2 1 4 25 x + y =

Question 3. 2 2 1 16 9 x + y =

Question 4. 2 2 1 25 100 x + y =

Question 5. 2 2 1 49 36 x + y =

Question 6. 100 400 x2 y2 + = 1

Question 7. 36x2 + 4y2 = 144

Question 8. 16x2 + y2 = 16

Question 9. 4x2 + 9y2 = 36 In each of the following Exercises 10 to 20, find the equation for the ellipse that satisfies the given conditions:

Question 10. Vertices (± 5, 0), foci (± 4, 0)

Question 11. Vertices (0, ± 13), foci (0, ± 5)

Question 12.Vertices (± 6, 0), foci (± 4, 0)

Question 13.Ends of major axis (± 3, 0), ends of minor axis (0, ± 2)

Question 14.Ends of major axis (0, ± 5 ), ends of minor axis (± 1, 0)

Question 15.Length of major axis 26, foci (± 5, 0)

Question 16.Length of minor axis 16, foci (0, ± 6).

Question 17. Foci (± 3, 0), a = 4

Question 18.b = 3, c = 4, centre at the origin; foci on a x axis.

Question 19.Centre at (0,0), major axis on the y-axis and passes through the points (3, 2) and (1,6).

Question 20. Major axis on the x-axis and passes through the points (4,3) and (6,2).

EXERCISE 11.4

In each of the Exercises 1 to 6, find the coordinates of the foci and the vertices, the eccentricity and the length of the latus rectum of the hyperbolas.

Question 1. 2 2 1 16 9 x – y =

Question 2. 2 2 1 9 27 y – x =

Question 3. 9y2 – 4x2 = 36

Question 4. 16x2 – 9y2 = 576

Question 5. 5y2 – 9x2 = 36

Question 6 .49y2 – 16x2 = 78 4 .In each of the Exercises 7 to 15, find the equations of the hyperbola satisfying the given conditions.

Question 7.Vertices (± 2, 0), foci (± 3, 0)

Question 8. Vertices (0, ± 5), foci (0, ± 8)

Question 9. Vertices (0, ± 3), foci (0, ± 5)

Question 10. Foci (± 5, 0), the transverse axis is of length 8.

Question 11.Foci (0, ±13), the conjugate axis is of length 2 4.

Question 2.Foci (± 3 5 , 0), the latus rectum is of length 8.

Question 3.Foci (± 4, 0), the latus rectum is of length 12.

Question 4.vertices (± 7,0), e = 3 4.

Question 5.Foci (0, ± 10 ), passing through (2,3)

Miscellaneous Exercise on Chapter 11

Question 1.If a parabolic reflector is 20 cm in diameter and 5 cm deep, find the focus.

Question 2.An arch is in the form of a parabola with its axis vertical. The arch is 10 m high and 5 m wide at the base. How wide is it 2 m from the vertex of the parabola?

Question 3.The cable of a uniformly loaded suspension bridge hangs in the form of a parabola. The roadway which is horizontal and 100 m long is supported by vertical wires attached to the cable, the longest wire being 30 m and the shortest being 6 m. Find the length of a supporting wire attached to the roadway 18 m from the middle.

Question 4.An arch is in the form of a semi-ellipse. It is 8 m wide and 2 m high at the centre. Find the height of the arch at a point 1.5 m from one end.

Question 5.A rod of length 12 cm moves with its ends always touching the coordinate axes. Determine the equation of the locus of a point P on the rod, which is 3 cm from the end in contact with the x-axis.

Question 6.Find the area of the triangle formed by the lines joining the vertex of the parabola x2 = 12y to the ends of its latus rectum.

Question 7.A man running a racecourse notes that the sum of the distances from the two flag posts from him is always 10 m and the distance between the flag posts is 8 m. Find the equation of the posts traced by the man.

Question 8.An equilateral triangle is inscribed in the parabola y2 = 4 ax, where one vertex is at the vertex of the parabola. Find the length of the side of the triangle.

---

(Mathematics) : Chapter 12 Introduction To Three Dimensional Geometry

---

EXERCISE 12.1

Question 1. A point is on the x-axis. What are its y-coordinate and z-coordinates?

Question 2.A point is in the XZ-plane. What can you say about its y-coordinate?

Question 3.Name the octants in which the following points lie:
(1,. 2, 3), (4, –2, 3), (4, –2, –5), (4, 2, –5), (– 4, 2, –5), (– 4, 2, 5), (–3, –1, 6) (2, – 4, –7).

Question 4.Fill in the blanks:
(i) The x-axis and y-axis taken together determine a plane known as_______.
(ii) The coordinates of points in the XY-plane are of the form _______.
(iii) Coordinate planes divide the space into ______ octants.

EXERCISE 12.2

Question 1. Find the distance between the following pairs of points:
(i) (2, 3, 5) and (4, 3, 1) (ii) (–3, 7, 2) and (2, 4, –1)
(iii) (–1, 3, – 4) and (1, –3, 4) (iv) (2, –1, 3) and (–2, 1, 3).

Question 2.Show that the points (–2, 3, 5), (1, 2, 3) and (7, 0, –1) are collinear.

Question 3.Verify the following:
(i) (0, 7, –10), (1, 6, – 6) and (4, 9, – 6) are the vertices of an isosceles triangle.
(ii) (0, 7, 10), (–1, 6, 6) and (– 4, 9, 6) are the vertices of a right angled triangle.
(iii) (–1, 2, 1), (1, –2, 5), (4, –7, 8) and (2, –3, 4) are the vertices of a parallelogram

Question 4.Find the equation of the set of points which are equidistant from the points (1, 2, 3) and (3, 2, –1).

Question 5.Find the equation of the set of points P, the sum of whose distances from A (4, 0, 0) and B (– 4, 0, 0) is equal to 10.

EXERCISE 12.3

Question 1. Find the coordinates of the point which divides the line segment joining the points (– 2, 3, 5) and (1, – 4, 6) in the ratio (i) 2 : 3 internally, (ii) 2 : 3 externally.

Question 2.Given that P (3, 2, – 4), Q (5, 4, – 6) and R (9, 8, –10) are collinear. Find the ratio in which Q divides PR.

Question 3.Find the ratio in which the YZ-plane divides the line segment formed by joining the points (–2, 4, 7) and (3, –5, 8).

Question 4.Using section formula, show that the points A (2, –3, 4), B (–1, 2, 1) and C 0 1 2 3 are collinear.

Question 5.Find the coordinates of the points which trisect the line segment joining the points P (4, 2, – 6) and Q (10, –16, 6).

Miscellaneous Exercise on Chapter 12

Question 1. Three vertices of a parallelogram ABCD are A(3, – 1, 2), B (1, 2, – 4) and C (– 1, 1, 2). Find the coordinates of the fourth vertex.

Question 2.Find the lengths of the medians of the triangle with vertices A (0, 0, 6), B (0,4, 0) and (6, 0, 0).

Question 3.If the origin is the centroid of the triangle PQR with vertices P (2a, 2, 6), Q (– 4, 3b, –10) and R(8, 14, 2c), then find the values of a, b and c.

Question 4.Find the coordinates of a point on y-axis which are at a distance of 5 2 from the point P (3, –2, 5).

Question 5.A point R with x-coordinate 4 lies on the line segment joining the points P(2, –3, 4) and Q (8, 0, 10). Find the coordinates of the point R. [Hint Suppose R divides PQ in the ratio k :1.The coordinates of the point R are given by , 10 4 1 , 3 1 8 2 k k k k k ]. .

---

(Mathematics) : Chapter 13 Limits And Derivatives

---

EXERCISE 13.1

Evaluate the following limits in Exercises 1 to 22.

Question 1. 3 lim 3 x x → +

Question 2. π lim 22 x 7 x →

Question 3. 2 1 limπ r r →

Question 4. 4 lim 4 3 x 2 x → x + −

Question 5. 10 5 1 lim 1 x 1 x x → − x + + −

Question 6. ( )5 0 1 1 lim x x → x + −

Question 7. 2 2 2 lim 3 10 x 4 x x → x − − −

Question 8. 4 3 2 lim 81 x 2 5 3 x → x x − − −

Question 9. 0 lim x 1 ax b → cx + +

Question 10. 1 3 1 1 6 lim 1 1 z z z → − −

Question 11. 2 1 2 lim , 0 x ax bx c a b c → cx bx a + + + + ≠ + +

Question 12. 2 1 1 lim 2 x 2 x →− x + +

Question 13. 0 lim sin x ax → bx

Question 14. 0 lim sin , , 0 x sin ax a b → bx ≠

Question 15. ( ) π ( ) sin π lim x π π x → x − −

Question 16. 0 lim cos x π x → − x

Question 17. 0 limcos 2 1 x cos 1 x → x − −

Question 18. 0 lim cos x sin ax x x → b x +

Question 19. 0 lim sec x x x →

Question 20. 0 lim sin , , 0 x sin ax bx a b a b → ax bx + + ≠ + ,

Question 21. 0 lim (cosec cot ) x x x → −

Question 22. π 2 lim tan 2π 2 x x → x −

Question 23. Find ( ) 0 lim x f x → and ( ) 1 lim x f x → , where ( ) ( ) 2 3, 0 3 1, 0 x x f x x x + ≤ = +>

Question 24. Find ( ) 1 lim x f x → , where ( ) 2 2 1, 1 1, 1 x x f x x x − ≤ = − − >

Question 25. Evaluate ( ) 0 lim x f x → , where ( ) | |, 0 0, 0 x x f x x x ≠ = =

Question 26. Find ( ) 0 lim x f x → , where ( ) , 0 | | 0, 0 x x f x x x ≠ = =

Question 27. Find ( ) 5 lim x f x → , where f (x) = | x | −5

Question 28. Suppose ( ) , 1 4, 1 , 1 a bx x fx x b ax x + <= = − > and if 1 lim x→ f (x) = f (1) what are possible values of a and b?

Question 29. Let a1, a2, . . ., an be fixed real numbers and define a function f (x) = (x − a1 ) (x − a2 )...(x − an ) . What is 1 lim x→a (x) ? For some a ≠ a1, a2, ..., an, compute lim x→a f (x).

Question 30. If ( ) 1, 0 0, 0 1, 0 x x f x x x x + < = = − > . For what value (s) of a does lim x→a f (x) exists?

Question 31. If the function f(x) satisfies ( ) 1 2 2 lim π x 1 f x → x − = − , evaluate ( ) 1 lim x f x → .

Question 32. If ( ) 2 3 , 0 , 0 1 , 1 mx n x f x nx m x nx m x + < = + ≤ ≤ + > . For what integers m and n does both ( ) 0 lim x f x → and ( ) 1 lim x f x → exist?

EXERCISE 13.2

Question 1. Find the derivative of x2 – 2 at x = 10.

Question 2. Find the derivative of 99x at x = l00.

Question 3. Find the derivative of x at x = 1.

Question 4. Find the derivative of the following functions from first principle.
(i) x3 − 27
(ii) (x −1)(x − 2)
(iii) 2 1 x
(iv) 1 1 x x + −

Question 5. For the function ( ) 100 99 2 .1 100 99 2 f x = x + x + + x + x + . Prove that f ′(1) =100 f ′(0) .

Question 6. Find the derivative of xn + axn−1 + a2 xn−2 + . . .+ an−1x + an for some fixed real number a.

Question 7. For some constants a and b, find the derivative of
(i) (x − a) (x − b)
(ii) ( )ax2 b 2 +
(iii) x a x b − −

Question 8. Find the derivative of xn an x a − − for some constant a.

Question 9. Find the derivative of
(i) 2 3 4 x −
(ii) (5x3 + 3x −1) (x −1)
(iii) x−3 (5 + 3x)
(iv) x5 (3 − 6x−9 )
(v) x−4 (3 − 4x−5 )
(vi) 2 2 1 3 1 x x x − + −

Question 10. Find the derivative of cos x from first principle.

Question 11. Find the derivative of the following functions:
(i) sin x cos x
(ii) sec x
(iii) 5sec x + 4cos x
(iv) cosec x
(v) 3cot x + 5cosec x
(vi) 5sin x − 6cos x + 7
(vii) 2tan x − 7sec x

---

(Mathematics) : Chapter 14 Mathematical Reasoning 

---

EXERCISE 14.1

Question 1.Which of the following sentences are statements? Give reasons for your answer.
(i) There are 35 days in a month.
(ii) Mathematics is difficult.
(iii) The sum of 5 and 7 is greater than 10.
(iv) The square of a number is an even number.
(v) The sides of a quadrilateral have equal length.
(vi) Answer this question.
(vii) The product of (–1) and 8 is 8.
(viii) The sum of all interior angles of a triangle is 180°.
(ix) Today is a windy day.
(x) All real numbers are complex numbers.

Question 2.Give three examples of sentences which are not statements. Give reasons for the answers.

EXERCISE 14.2

Question 1.Write the negation of the following statements:
(i) Chennai is the capital of Tamil Nadu
(ii) 2 is not a complex number
(iii) All triangles are not equilateral triangle
(iv) The number 2 is greater than 7.
(v) Every natural number is an integer.

Question 2.Are the following pairs of statements negations of each other:
(i) The number x is not a rational number. The number x is not an irrational number.
(ii) The number x is a rational number. The number x is an irrational number.

Question 3.Find the component statements of the following compound statements and check whether they are true or false.
(i) Number 3 is prime or it is odd.
(ii) All integers are positive or negative.
(iii) 100 is divisible by 3, 11 and 5.

EXERCISE 14.3

Question 1.For each of the following compound statements first identify the connecting words and then break it into component statements.
(i) All rational numbers are real and all real numbers are not complex.
(ii) Square of an integer is positive or negative.
(iii) The sand heats up quickly in the Sun and does not cool down fast at night.
(iv) x = 2 and x = 3 are the roots of the equation 3x2 – x – 10 = 0.

Question 2.Identify the quantifier in the following statements and write the negation of the statements.
(i) There exists a number which is equal to its square.
(ii) For every real number x, x is less than x +1.
(iii) There exists a capital for every state in India.

Question 3.Check whether the following pair of statements are negation of each other. Give reasons for your answer.
(i) x + y = y + x is true for every real numbers x and y.
(ii) There exists real numbers x and y for which x + y = y + x. 4. State whether the “Or” used in the following statements is “exclusive “or” inclusive. Give reasons for your answer.
(i) Sun rises or Moon sets.
(ii) To apply for a driving licence, you should have a ration card or a passport.
(iii) All integers are positive or negative. 

EXERCISE 14.4

Question 1.Rewrite the following statement with “if-then” in five different ways conveying the same meaning. If a natural number is odd, then its square is also odd.

Question 2.Write the contrapositive and converse of the following statements.
(i) If x is a prime number, then x is odd. (ii) If the two lines are parallel, then they do not intersect in the same plane.
(iii) Something is cold implies that it has low temperature.
(iv) You cannot comprehend geometry if you do not know how to reason deductively.
(v) x is an even number implies that x is divisible by 4.

Question 3.Write each of the following statements in the form “if-then”
(i) You get a job implies that your credentials are good.
(ii) The Bannana trees will bloom if it stays warm for a month.
(iii) A quadrilateral is a parallelogram if its diagonals bisect each other.
(iv) To get an A+ in the class, it is necessary that you do all the exercises of the book.

Question 4.Given statements in (a) and (b). Identify the statements given below as contrapositive or converse of each other. (a) If you live in Delhi, then you have winter clothes.
(i) If you do not have winter clothes, then you do not live in Delhi.
(ii) If you have winter clothes, then you live in Delhi.
(b) If a quadrilateral is a parallelogram, then its diagonals bisect each other.
(i) If the diagonals of a quadrilateral do not bisect each other, then the quadrilateral is not a parallelogram.
(ii) If the diagonals of a quadrilateral bisect each other, then it is a parallelogram. 

EXERCISE 14.5

Question 1.Show that the statement p: “If x is a real number such that x3 + 4x = 0, then x is 0” is true by
(i) direct method,
(ii) method of contradiction,
(iii) method of contrapositive

Question 2.Show that the statement “For any real numbers a and b, a2 = b2 implies that a = b” is not true by giving a counter-example.

Question 3.Show that the following statement is true by the method of contrapositive. p: If x is an integer and x2 is even, then x is also even.

Question 4.By giving a counter example, show that the following statements are not true.
(i) p: If all the angles of a triangle are equal, then the triangle is an obtuse angled triangle.
(ii) q: The equation x2 – 1 = 0 does not have a root lying between 0 and 2.

Question 5.Which of the following statements are true and which are false? In each case give a valid reason for saying so.
(i) p: Each radius of a circle is a chord of the circle.
(ii) q: The centre of a circle bisects each chord of the circle.
(iii) r: Circle is a particular case of an ellipse.
(iv) s: If x and y are integers such that x > y, then –x < – y. (v) t : 11 is a rational number.

Miscellaneous Exercise on Chapter 14

Question 1.Write the negation of the following statements:
(i) p: For every positive real number x, the number x – 1 is also positive.
(ii) q: All cats scratch.
(iii) r: For every real number x, either x > 1 or x <1.
(iv) s: There exists a number x such that 0 < x <1.

Question 2.State the converse and contrapositive of each of the following statements:
(i) p: A positive integer is prime only if it has no divisors other than 1 and itself .
(ii) q: I go to a beach whenever it is a sunny day.
(iii) r: If it is hot outside, then you feel thirsty.

Question 3.Write each of the statements in the form “if p, then q”
(i) p: It is necessary to have a password to log on to the server.
(ii) q: There is traffic jam whenever it rains.
(iii) r: You can access the website only if you pay a subsciption fee.

Question 4.Rewrite each of the following statements in the form “p if and only if q”
(i) p: If you watch television, then your mind is free and if your mind is free, then you watch television.
(ii) q: For you to get an A grade, it is necessary and sufficient that you do all the homework regularly.
(iii) r: If a quadrilateral is equiangular, then it is a rectangle and if a quadrilateral is a rectangle, then it is equiangular.

Question 5.Given below are two statements p :
25 is a multiple of 5.q : 25 is a multiple of 8. Write the compound statements connecting these two statements with “And” and “Or”. In both cases check the validity of the compound statement.

Question 6. Check the validity of the statements given below by the method given against it.
(i) p: The sum of an irrational number and a rational number is irrational (by contradiction method).
(ii) q: If n is a real number with n > 3, then n2 > 9 (by contradiction method).

Question 7. Write the following statement in five different ways, conveying the same meaning. p: If a triangle is equiangular, then it is an obtuse angled triangle. 

---

 (Mathematics) : Chapter 15 Statistics

---

EXERCISE 15.1

Find the mean deviation about the mean for the data in Exercises 1 and 2.

Question 1. 4, 7, 8, 9, 10, 12, 13, 17

Question 2. 38, 70, 48, 40, 42, 55, 63, 46, 54, 44

Find the mean deviation about the median for the data in Exercises 3 and 4.

Question 3. 13, 17, 16, 14, 11, 13, 10, 16, 11, 18, 12, 17

Question 4. 36, 72, 46, 42, 60, 45, 53, 46, 51, 49

Find the mean deviation about the mean for the data in Exercises 5 and 6.

Question 5. xi 5 10 15 20 25 f i 7 4 6 3 5

Question 6. xi 10 30 50 70 90 f i 4 24 28 16 8

Find the mean deviation about the median for the data in Exercises 7 and 8.

Question 7. xi 5 7 9 10 12 15 f i 8 6 2 2 2 6

Question 8. xi 15 21 27 30 35 f i 3 5 6 7 8

Find the mean deviation about the mean for the data in Exercises 9 and 10.

Question 9. Income 0-100 100-200 200-300 300-400 400-500 500-600 600-700 700-800
per day Number 4 8 9 10 7 5 4 3
of persons

Question 10. Height 95-105 105-115 115-125 125-135 135-145 145-155
in cms
Number of 9 13 26 30 12 10
boys

Question 11. Find the mean deviation about median for the following data :
Marks 0-10 10-20 20-30 30-40 40-50 50-60
Number of 6 8 14 16 4 2
Girls

Question 12. Calculate the mean deviation about median age for the age distribution of 100 persons given below:
Age 16-20 21-25 26-30 31-35 36-40 41-45 46-50 51-55
Number 5 6 12 14 26 12 16 9

EXERCISE 15.2

Find the mean and variance for each of the data in Exercies 1 to 5.

Question 1. 6, 7, 10, 12, 13, 4, 8, 12

Question 2. First n natural numbers

Question 3. First 10 multiples of 3

Question 4. xi 6 10 14 18 24 28 30 fi 2 4 7 12 8 4 3

Question 5. xi 92 93 97 98 102 104 109 f i 3 2 3 2 6 3 3

Question 6. Find the mean and standard deviation using short-cut method.
xi 60 61 62 63 64 65 66 67 68
f i 2 1 12 29 25 12 10 4 5

Find the mean and variance for the following frequency distributions in Exercises 7 and 8.

Question 7. Classes 0-30 30-60 60-90 90-120 120-150 150-180 180-210
Frequencies 2 3 5 10 3 5 2

Question 8. Classes 0-10 10-20 20-30 30-40 40-50
Frequencies 5 8 15 16 6

Question 9. Find the mean, variance and standard deviation using short-cut method
Height 70-75 75-80 80-85 85-90 90-95 95-100 100-105105-110 110-115
in cms No. of 3 4 7 7 15 9 6 6 3
children

Question 10. The diameters of circles (in mm) drawn in a design are given below:
Diameters 33-36 37-40 41-44 45-48 49-52 No. of circles 15 17 21 22 25 Calculate the standard deviation and mean diameter of the circles.[ Hint First make the data continuous by making the classes as 32.5-36.5, 36.5-40.5, 40.5-44.5, 44.5 - 48.5, 48.5 - 52.5 and then proceed.]

EXERCISE 15.3

Question 1. From the data given below state which group is more variable, A or B?
Marks 10-20 20-30 30-40 40-50 50-60 60-70 70-80
Group A 9 17 32 33 40 10 9
Group B 10 20 30 25 43 15 7

Question 2. From the prices of shares X and Y below, find out which is more stable in value:
X 35 54 52 53 56 58 52 50 51 49
Y 108 107 105 105 106 107 104 103 104 101

Question 3. An analysis of monthly wages paid to workers in two firms A and B, belonging to the same industry, gives the following results: Firm A Firm B No. of wage earners 586 648 Mean of monthly wages Rs 5253 Rs 5253 Variance of the distribution 100 121 of wages
(i) Which firm A or B pays larger amount as monthly wages?
(ii) Which firm, A or B, shows greater variability in individual wages?

Question 4. The following is the record of goals scored by team A in a football session:
No. of goals scored 0 1 2 3 4
No. of matches 1 9 7 5 3
For the team B, mean number of goals scored per match was 2 with a standard deviation 1.25 goals. Find which team may be considered more consistent?

Question 5. The sum and sum of squares corresponding to length x (in cm) and weight y (in gm) of 50 plant products are given below: 50 1 i 212 i x = Σ = , 50 2 1 i 902 8 i x . = Σ = , 50 1 i 261 i y = Σ = , 50 2 1 i 1457 6 i y . = Σ = Which is more varying, the length or weight?

---

 (Mathematics) : Chapter 16 Probability

---

  EXERCISE 16.1

1 to 7, describe the sample space for the indicated experiment.

Question 1.A coin is tossed three times.

Question 2.A die is thrown two times.

Question 3.A coin is tossed four times.

Question 4.A coin is tossed and a die is thrown.

Question 5.A coin is tossed and then a die is rolled only in case a head is shown on the coin

Question 6.2 boys and 2 girls are in Room X, and 1 boy and 3 girls in Room Y. Specify the sample space for the experiment in which a room is selected and then a person.

Question 7. One die of red colour, one of white colour and one of blue colour are placed in a bag. One die is selected at random and rolled, its colour and the number on its uppermost face is noted. Describe the sample space.

Question 8. An experiment consists of recording boy–girl composition of families with 2 children.
(i) What is the sample space if we are interested in knowing whether it is a boy or girl in the order of their births?
(ii) What is the sample space if we are interested in the number of girls in the family?

Question 9.A box contains 1 red and 3 identical white balls. Two balls are drawn at random in succession without replacement. Write the sample space for this experiment.

Question 10. An experiment consists of tossing a coin and then throwing it second time if a head occurs. If a tail occurs on the first toss, then a die is rolled once. Find the sample space.

Question 11.Suppose 3 bulbs are selected at random from a lot. Each bulb is tested and classified as defective (D) or non – defective(N). Write the sample space of this experiment.

Question 12.A coin is tossed. If the out come is a head, a die is thrown. If the die shows up an even number, the die is thrown again. What is the sample space for the experiment?

Question 13.The numbers 1, 2, 3 and 4 are written separatly on four slips of paper. The slips are put in a box and mixed thoroughly. A person draws two slips from the box, one after the other, without replacement. Describe the sample space for the experiment.

Question 14.An experiment consists of rolling a die and then tossing a coin once if the number on the die is even. If the number on the die is odd, the coin is tossed twice. Write the sample space for this experiment.

Question 15.A coin is tossed. If it shows a tail, we draw a ball from a box which contains 2 red and 3 black balls. If it shows head, we throw a die. Find the sample space for this experiment.

Question&nbsnbsp;16.A die is thrown repeatedly untill a six comes up. What is the sample space for this experiment?

EXERCISE 16.2

Question 1.A die is rolled. Let E be the event “die shows 4” and F be the event “die shows even number”. Are E and F mutually exclusive?

Question 2.A die is thrown. Describe the following events
(i) A: a number less than 7
(ii) B: a number greater than 7
(iii) C: a multiple of 3
(iv) D: a number less than 4
(v) E: an even number greater than 4
(vi) F: a number not less than 3 Also find A ∪ B, A ∩ B, E ∪ F, D ∩ E, A – C, D – E, F′, E ∩ F′,

Question 3.An experiment involves rolling a pair of dice and recording the numbers that come up. Describe the following events: A: the sum is greater than 8, B: 2 occurs on either die C: the sum is at least 7 and a multiple to 3 Which pairs of these events are mutually exclusive?

Question 4.Three coins are tossed once. Let A denote the event ‘three heads show”, B denote the event “two heads and one tail show”, C denote the event” three tails show and D denote the event ‘a head shows on the first coin”. Which events are
(i) mutually exclusive?
(ii) simple?
(iii) Compound?

Question 5.Three coins are tossed. Describe
(i) Two events which are mutually exclusive .
(ii) Three events which are mutually exclusive and exhaustive.
(iii) Two events, which are not mutually exclusive.
(iv) Two events which are mutually exclusive but not exhaustive.
(v) Three events which are mutually exclusive but not exhaustive.

Question 6.Two dice are thrown. The events A, B and C are as follows: A: getting an even number on the first die. B: getting an odd number on the first die. C: getting the sum of the numbers on the dice ≤

Question 5.Describe the events
(i) A′
(ii) not B
(iii) A or B
(iv) A and B
(v) A but not C
(vi) B or C
(vii) B and C
(viii) A ∩ B′ ∩ C′

Question 7. Refer to question 6 above, state true or false: (give reason for your answer)
(i) A and B are mutually exclusive
(ii) A and B are mutually exclusive and exhaustive
(iii) A = B′
(iv) A and C are mutually exclusive (v) A and B′ are mutually exclusive. (vi) A′, B′, C are mutually exclusive and exhaustive.

EXERCISE 16.3

Question 1.Which of the following can not be valid assignment of probabilities for outcomes of sample Space S = { } ω1,ω2 ,ω3,ω4 ,ω5 ,ω6 ,ω7

Question 2.A coin is tossed twice, what is the probability that atleast one tail occurs?

Question 3.A die is thrown, find the probability of following events:
(i) A prime number will appear,
(ii) A number greater than or equal to 3 will appear,
(iii) A number less than or equal to one will appear,
(iv) A number more than 6 will appear,
(v) A number less than 6 will appear.

Question 4.A card is selected from a pack of 52 cards .
(a) How many points are there in the sample space?
(b) Calculate the probability that the card is an ace of spades.
(c) Calculate the probability that the card is
(i) an ace
(ii) black card.

Question 5.A fair coin with 1 marked on one face and 6 on the other and a fair die are both tossed. find the probability that the sum of numbers that turn up is
(i) 3
(ii) 12

Question 6.There are four men and six women on the city council. If one council member is selected for a committee at random, how likely is it that it is a woman?

Question 7. A fair coin is tossed four times, and a person win Re 1 for each head and lose Rs 1.50 for each tail that turns up. From the sample space calculate how many different amounts of money you can have after four tosses and the probability of having each of these amounts.

Question 8.Three coins are tossed once. Find the probability of getting
(i) 3 heads
(ii) 2 heads
(iii) atleast 2 heads
(iv) atmost 2 heads
(v) no head
(vi) 3 tails
(vii) exactly two tails
(viii) no tail
(ix) atmost two tails

Question 9.If 11 2 is the probability of an event, what is the probability of the event ‘not A’.

Question 10.A letter is chosen at random from the word ‘ASSASSINATION’. Find the probability that letter is
(i) a vowel
(ii) a consonan

Question 11.In a lottery, a person choses six different natural numbers at random from 1 to 20, and if these six numbers match with the six numbers already fixed by the lottery committee, he wins the prize. What is the probability of Winning the prize in the game. [Hint order of the numbers is not important.]

Question 12.Given P(A) = 5 3 and P(B) = 51. Find P(A or B), if A and B are mutually exclusive events.

Question 13.If E and F are events such that P(E) = 4 1 , P(F) = 2 1 and P(E and F) = 8 1 , find
(i) P(E or F),
(ii) P(not E and not F).

Question 14.Events E and F are such that P(not E or not F) = 0.25, State whether E and F are mutually exclusive.

Question 15. A and B are events such that P(A) = 0.42, P(B) = 0.48 and P(A and B) = 0

Question 6.Determine
(i) P(not A)
(ii) P(not B) and
(iii) P(A or B)

Question 16. In Class XI of a school 40% of the students study Mathematics and 30% study Biology. 10% of the class study both Mathematics and Biology. If a student is selected at random from the class, find the probability that he will be studying Mathematics or Biology.

Question 17. In an entrance test that is graded on the basis of two examinations, the probability of a randomly chosen student passing the first examination is 0.8 and the probability of passing the second examination is 0. 7. The probability of passing atleast one of them is 0.99. What is the probability of passing both?

Question 18. The probability that a student will pass the final examination in both English and Hindi is 0.5 and the probability of passing neither is 01. If the probability of passing the English examination is 0.75, what is the probability of passing the Hindi examination?

Question 20.In a class of 60 students, 30 opted for NCC, 32 opted for NSS and 24 opted for both NCC and NSS. If one of these students is selected at random, find the probability that
(i) The student opted for NCC or NSS.
(ii) The student has opted neither NCC nor NSS.
(iii) The student has opted NSS but not NCC.

 

Click Here to Download Full Paper

---

  <<Go Back To Main Page