(Paper) CBSE Class XII : Mathematic Exam Paper Year 2009 (Delhi)
Disclaimer: This website is NOT associated with CBSE, for official website of CBSE visit - www.cbse.gov.in
CBSE Class XII : Mathematic Exam Paper Year 2009 (Delhi)
- Time allowed : 3 hours
- Maximum marks: 100
General Instructions:
(i) All questions are compulsory.
(ii) The question paper consists of 29 questions divided into three Sections A,
B and C. Section A comprises of 10 questions of one marks each, Section B
comprises of 12 questions of four marks each and Section C comprises of 7
questions of six marks each.
(iii) All questions in Section A are to be answered in one word, one sentence or
as per the exact requirement of the question.
(iv) There is no overall choice. However, internal choice has been provided in 4
questions of four marks each and 2 questions of six marks each. You have to
attempt only one of the alternatives in all such questions.
(v) Use of calculators is not permitted.
SECTION –A
Question number 1 to 10 carry one mark each.

4. If matrix A = (1 2 3), write AA’, where A’ is the transpose of matrix A.

6. Using principal value, evaluate the following: sin-1(sin
3π/5)
7. Evaluate : ∫ [sec2x/(3 + tanx) ]dx
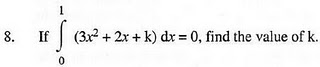
9. If the binary operation * on the set of integers Z, is
defined by a * b = a + 3b2, then find the value of 2 * 4.
10. If A is an invertible matrix of order 3 and |A| = 5, then find |adj
A|.
SECTION – B
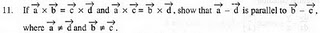
12. Prove that sin-1(4/5) + sin-1(5/13) + sin-1(16/65) = π/2
OR
Solve for x : tan-13x + tan-12x = π/4
13. Find the value of λ so that the lines (1 – x)/3 = (7y –
14)/2λ = (5z – 10)/11 and (7 – 7x)/3λ = (y – 5)/1 = (6 – z)/5 are perpendicular
to each other.
14. Solve the following differential equation: dy/dx + y =
cos x – sin x.
15. Find the particular solution, satisfying the given condition, for
the following differential equation:
dy/dx – y/x + coses (y/x) = 0; y = 0 when x = 1.
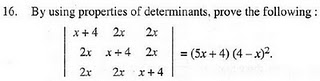
17. A die is thrown again and again until three sixes are
obtained. Find the probability of obtaining the third six in the sixth throw of
the die.
18. Differentiate the following function w.r.t. x: xsin x +
(sin x)cos x .
19. Evaluate : ∫ [ex/√(5 – 4 ex – e2x)]dx
OR
Evaluate : ∫ [{(x - 4)ex}/(x - 2)3]dx.
20. Prove that the relation R in the set A = {1, 2, 3, 4, 5}
given by = {(a, b): |a – b| is even}, is an equivalence relation.
21. Find dy/dx if (x2 + y2)2 = xy
OR
If y = 3 cos(log x) + 4 sin (log x), then show that x2.d2y/dx + x.dy/dx + y = 0
22. Find the equation of the tangent to the curve y = √(3x-2) which is parallel to the line 4x – 2y + 5 = 0.
OR
Find the intervals in which the function f given by f(x) = x3 + 1/x3, x ≠ 0 is (i) increasing (ii) decreasing.
SECTION – C
23. Find the volume of the largest cylinder that can be inscribed in a sphere of redius r.
OR
A tank with rectangular base and rectangular sides, open at the top is to be constructed so that its depth is 2 m and volume is 8 m3, If building of tank costs Rs. 70 per sq. Metre for base and Rs. 45 per sq. Metre for sides, what is the cost of least expensive tank?
24. A diet is to contain at least 80 units of vitamin A and 100 units of minerals. Two foods F1 and F2 are available. Food F1 costs Rs. 4 per unit and F2 costs Rs. 6 per unit. One unit of food F1 contains 3 units of Vitamin A and 4 units of minerals. One unit of food F2 contains 6 units of Vitamin and 3 units of minerals. Formulate this as a linear programming problem and find graphically the minimum cost for diet that consists of mixture of these two foods and also meets the minimal nutritional requirements.
25. Three bags contain balls as shown in the table below:
| Bag | Number of White balls | Number of Black Balls | Number of Red balls |
| I | 1 | 2 | 6 |
| II | 2 | 1 | 1 |
| III | 4 | 3 | 2 |
A bag is chosen at random and two balls are drawn from it. They happen to be white and red. What is the probability that they came from the III bag?
26. Using matrices, solve the following system of equations:
2x – 3y + 5z = 11
3x + 2y – 4z = -5
X + y – 2z = –3
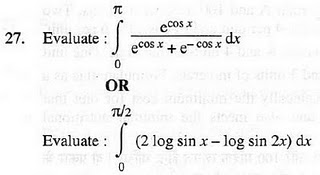
28. Using the method of integration, find the area of the
region bounded by the lines 2x + y = 4, 3x – 2y = 6 and x – 3y + 5 = 0 .
29. Find the equation of the plane passing through the point (-1, 3, 2)
and perpendicular to each of the planes x + 2y + 3z = 5 and 3x + 3y + z = 0.