NCERT Mathematics Question Paper (Class - 12)
Disclaimer: This website is NOT associated with CBSE, for official website of CBSE visit - www.cbse.gov.in

NCERT Mathematics Question Paper (Class - 12)
:: Chapter 1 - Number System ::
Q1. Determine whether each of the following relations are reflexive, symmetric and transitive:
(ii) Relation R in the set N of natural numbers defined as
R = {(x, y) : y = x + 5 and x < 4}
(iii) Relation R in the set A = {1, 2, 3, 4, 5, 6} as
R = {(x, y) : y is divisible by x}
(iv) Relation R in the set Z of all integers defined as
R = {(x, y) : x – y is an integer}
Q 1. Determine whether each of the following relations are reflexive,
symmetric and transitive:
(i) Relation R in the set A = {1, 2, 3, ..., 13, 14} defined
as
R = {(x, y) : 3x – y = 0}
Q 1.Determine whether each of the following relations are reflexive,
symmetric and transitive:
(v) Relation R in the set A of human beings in a town at a particular time given by
(a) R = {(x, y) : x and y work at the same place}
(b) R = {(x, y) : x and y live in the same locality}
(c) R = {(x, y) : x is exactly 7 cm taller than y}
(d) R = {(x, y) : x is wife of y}
(e) R = {(x, y) : x is father of y}
2. Show that the relation R in the set R of real numbers, defined as
R = {(a, b) : a ? b2} is neither reflexive nor symmetric nor transitive.
3. Check whether the relation R defined in the set {1, 2, 3, 4, 5, 6} as
R = {(a, b) : b = a + 1} is reflexive, symmetric or transitive.
4. Show that the relation R in R defined as R = {(a, b) : a ? b}, is reflexive
and transitive but not symmetric.
5. Check whether the relation R in R defined by R = {(a, b) : a ? b3} is
reflexive, symmetric or transitive.
6. Show that the relation R in the set {1, 2, 3} given by R = {(1, 2), (2, 1)}
is symmetric but neither reflexive nor transitive.
7. Show that the relation R in the set A of all the books in a library of a
college, given by R = {(x, y) : x and y have same number of pages} is an
equivalence relation.
8. Show that the relation R in the set A = {1, 2, 3, 4, 5} given by
R = {(a, b) : |a – b| is even}, is an equivalence relation. Show that all
the elements of {1, 3, 5} are related to each other and all the elements of {2,
4} are related to each other. But no element of {1, 3, 5} is related to any
element of {2, 4}.
9. Show that each of the relation R in the set A = {x ? Z : 0 ? x ? 12},
given by
(i) R = {(a, b) : |a – b| is a multiple of 4}
(ii) R = {(a, b) : a = b}
:: Chapter 2 - Inverse Trigonometric Functions ::
EXERCISE
Question 1. Find the principal values of the following:

Question 6. Show that the relation R in the set {1, 2, 3} given by R = {(1, 2), (2, 1)} is symmetric but neither reflexive nor transitive.
Question 7. Show that the relation R in the set A of all the books in a library of a college, given by R = {(x, y) : x and y have same number of pages} is an equivalence relation.
Question 8. Show that the relation R in the set A = {1, 2,
3, 4, 5} given by R = {(a, b) :
|a – b| is even}, is an equivalence relation. Show that all the elements of
{1, 3, 5} are related to each other and all the elements of {2, 4} are related
to each other. But no element of {1, 3, 5} is related to any element of {2, 4}.
Question 9. Show that each of the relation R in the set A = {x ∈ Z : 0 ≤ x ≤ 12}, given by (i) R = {(a, b) : |a – b| is a multiple of 4} (ii) R = {(a, b) : a = b} is an equivalence relation. Find the set of all elements related to 1 in each case.
Question 10. Give an example of a relation. Which is
(i) Symmetric but neither reflexive nor transitive.
(ii) Transitive but neither reflexive nor symmetric.
(iii) Reflexive and symmetric but not transitive.
(iv) Reflexive and transitive but not symmetric.
(v) Symmetric and transitive but not reflexive.
Question 11. Show that the relation R in the set A of points in a plane given by R = {(P, Q) : distance of the point P from the origin is same as the distance of the point Q from the origin}, is an equivalence relation. Further, show that the set of all points related to a point P ≠ (0, 0) is the circle passing through P with origin as centre.
Question 12. Show that the relation R defined in the set A of all triangles as R = {(T1, T2) : T1 is similar to T2}, is equivalence relation. Consider three right angle triangles T1 with sides 3, 4, 5, T2 with sides 5, 12, 13 and T3 with sides 6, 8, 10. Which triangles among T1, T2 and T3 are related?
Question 13. Show that the relation R defined in the set A of all polygons as R = {(P1, P2) : P1 and P2 have same number of sides}, is an equivalence relation. What is the set of all elements in A related to the right angle triangle T with sides 3, 4 and 5?
Question 14. Let L be the set of all lines in XY plane and R be the relation in L defined as R = {(L1, L2) : L1 is parallel to L2}. Show that R is an equivalence relation. Find the set of all lines related to the line y = 2x + 4.
Question 15. Let R be the relation in the set {1, 2, 3, 4}
given by R = {(1, 2), (2, 2), (1, 1), (4,4), (1, 3), (3, 3), (3, 2)}. Choose the
correct answer.
(A) R is reflexive and symmetric but not transitive.
(B) R is reflexive and transitive but not symmetric.
(C) R is symmetric and transitive but not reflexive.
(D) R is an equivalence relation.
Question 16. Let R be the relation in the set N given by R
= {(a, b) : a = b – 2, b > 6}. Choose the correct answer.
(A) (2, 4) ∈ R
(B) (3, 8) ∈ R
(C) (6, 8) ∈ R
(D) (8, 7) ∈ R
EXERCISE
Question 1. Show that the function f : R → R defined by f (x) = 1 x is one-one and onto, where R is the set of all non-zero real numbers. Is the result true, if the domain R is replaced by N with co-domain being same as R?
Question 2. Check the injectivity and surjectivity of the following functions:
(i) f : N → N given by f (x) = x2
(ii) f : Z → Z given by f (x) = x2
(iii) f : R → R given by f (x) = x2
(iv) f : N → N given by f (x) = x3
(v) f : Z → Z given by f (x) = x3
Question 3. Prove that the Greatest Integer Function f :
R→R, given by f (x) = [x], is neither one-one nor onto, where [x] denotes
the greatest integer less than or equal to x.
Question 4. Show that the Modulus Function f : R→R, given by f (x) = | x |, is neither oneone nor onto, where | x | is x, if x is positive or 0 and | x | is – x, if x is negative. 5. Show that the Signum Function f : R→R, given by
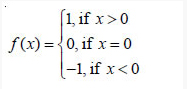
is neither one-one nor onto.
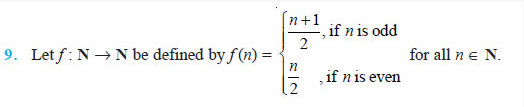
State whether the function f is bijective. Justify your answer.
Question 10. Let A = R – {3} and B = R – {1}. Consider the function f : A → B defined by

Question 11. Let f : R → R be defined as f(x) = x4. Choose
the correct answer.
(A) f is one-one onto (B) f is many-one onto
(C) f is one-one but not onto
(D) f is neither one-one nor onto.
Question 12. Let f : R → R be defined as f (x) = 3x.
Choose the correct answer.
(A) f is one-one onto
(B) f is many-one onto
(C) f is one-one but not onto
(D) f is neither one-one nor onto.
EXERCISE

 EXERCISE
EXERCISE



Show that is commutative and associative. Find the identity element for on A, if any.
Question 12. State whether the following statements are true or false. Justify.
(i) For an arbitrary binary operation on a set N, a a = a ∀ a
∈ N.
(ii) If is a commutative binary operation on N, then a (b c) = (c b) a
Question 13. Consider a binary operation on N defined as a b = a3 + b3. Choose the correct answer.
(A) Is both associative and commutative?
(B) Is commutative but not associative?
(C) Is associative but not commutative?
(D) Is neither commutative nor associative?

Define the relation R in P(X) as follows: For subsets A, B in P(X), ARB if and only if A ⊂ B. Is R an equivalence relation on P(X)? Justify your answer.
Question 9. Given a non-empty set X, consider the binary operation :
P(X) × P(X) → P(X) given by A B = A ∩ B ∀ A, B in P(X), where P(X) is the power set of X. Show that X is the identity element for this operation and X is the only invertible element in P(X) with respect to the operation
Question 10. Find the number of all onto functions from the set {1, 2, 3, ... , n} to itself.
Question 11. Let S = {a, b, c} and T = {1, 2, 3}. Find F–1
of the following functions F from S to T, if it exists.
(i) F = {(a, 3), (b, 2), (c, 1)}
(ii) F = {(a, 2), (b, 1), (c, 1)}
Question 12. Consider the binary operations : R × R → R and o : R × R → R defined as a b = |a – b| and a o b = a, ∀ a, b ∈ R. Show that is commutative but not associative, o is associative but not commutative. Further, show that ∀ a, b, c ∈ R, a (b o c) = (a b) o (a b). [If it is so, we say that the operation distributes over the operation o]. Does o distribute over ? Justify your answer.
Question 13. Given a non-empty set X, let : P(X) × P(X) → P(X) be defined as A * B = (A – B) ∪ (B – A), ∀ A, B ∈ P(X). Show that the empty set φ is the identity for the operation and all the elements A of P(X) are invertible with A–1 = A. (Hint : (A – φ) ∪ (φ – A) = A and (A – A) ∪ (A – A) = A A = φ).
Question 14. Define a binary operation on the set {0, 1, 2, 3, 4, 5} as



:: Chapter 3 - Matrix ::
EXERCISE
Question 1. In the matrix
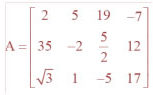 , write
, write
(i) The order of the matrix, (ii) The number of elements,
(iii) Write the elements a13, a21, a33, a24, a23.
Question 2. If a matrix has 24 elements, what are the possible orders it can have? What, if it has 13 elements?
Question 3. If a matrix has 18 elements, what are the possible orders it can have? What, if it has 5 elements ?
Question 4. Construct a 2 × 2 matrix, A = [aij], whose
elements are given by:
(i)aij=(i + j)2/2
Question 4. Construct a 2 × 2 matrix, A = [aij], whose
elements are given by:
(ii)aij=i/j
Question 4. Construct a 2 × 2 matrix, A = [aij], whose
elements are given by:
(iii)aij=(i + 2j)2/2
Question 5. Construct a 3 × 4 matrix, whose elements are
given by:
(i)aij=1/2| -3i + j |
Question 5. Construct a 3 × 4 matrix, whose elements are
given by:
(ii)aij=2i - j
Question 6. Find the values of x, y and z from the following equations:
(i)
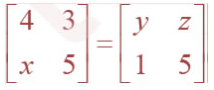
Question 6. Find the values of x, y and z from the following equations:
(ii)
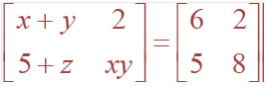
Question 6. Find the values of x, y and z from the following equations:
(iii)
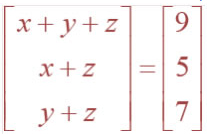
Question 7. Find the value of a, b, c and d from the equation
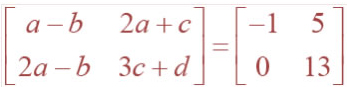
Question 8
![]() .is a
square matrix, if
.is a
square matrix, if
(A) m < n (B) m > n (C) m = n (D) None of these
Question 9.Which of the given values of x and y make the
following pair of matrices equal
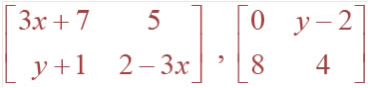
Question 10. The number of all possible matrices of order 3 × 3 with each entry 0 or 1 is:
EXERCISE
=Question 1. Let
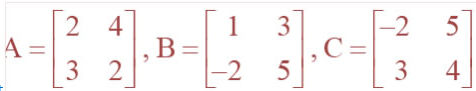 Find
each of the following:
Find
each of the following:
(i) A + B (ii) A – B (iii) 3A – C
=Question 1. Let
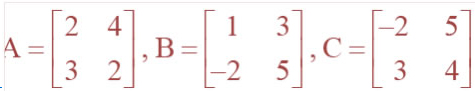 Find
each of the following:
Find
each of the following:
(iv) AB (v) BA
=Question 2. Compute the following:
=Question 3. Compute the indicated products.
=Question 4.
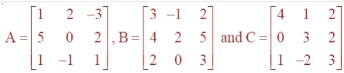 If ,
then compute (A+B) and (B – C). Also, verify that A + (B – C) = (A + B) – C.
If ,
then compute (A+B) and (B – C). Also, verify that A + (B – C) = (A + B) – C.
=Question 5.
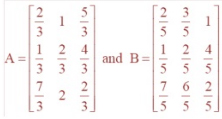 If ,
then compute 3A – 5B.
If ,
then compute 3A – 5B.
=Question 6. Simplify
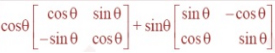
:: Chapter 4 - Determinants ::
Exercise
Question 1. Evaluate the determinants in Exercises 1 and 2.
Question 2. Evaluate the determinants in Exercises 1 and 2.
Question 3. If
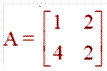 ,
then show that | 2A | = 4 | A |
,
then show that | 2A | = 4 | A |
Question 4. If
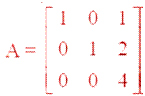 ,
then show that | 3 A | = 27 | A |
,
then show that | 3 A | = 27 | A |
Question 5. Evaluate the determinants
Question 6. If
 ,
find | A |
,
find | A |
Question 7. Find values of x, if

Question 8. If
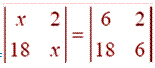 ,
then x is equal to
,
then x is equal to
Exercise
Using the property of determinants and without expanding in
Exercises 1 to 7, prove That
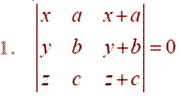
Using the property of determinants and without expanding in Exercises 1 to 7,
prove That
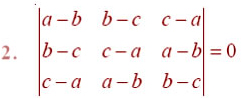
Using the property of determinants and without expanding in Exercises 1 to 7,
prove That
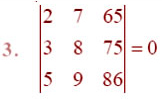
Using the property of determinants and without expanding in Exercises 1 to 7,
prove That
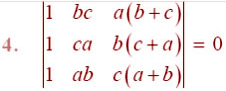
Using the property of determinants and without expanding in Exercises 1 to 7,
prove That
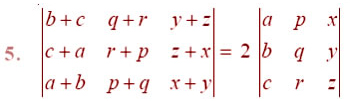
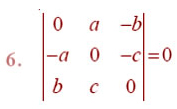
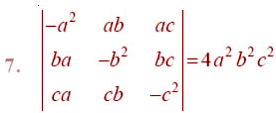
By using properties of determinants, in Exercises 8 to 14, show that:
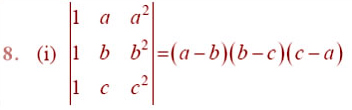
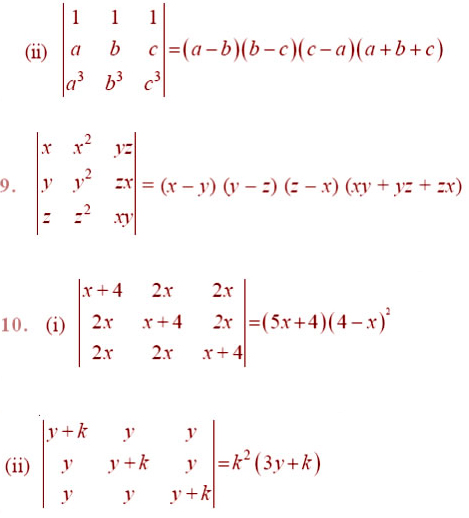
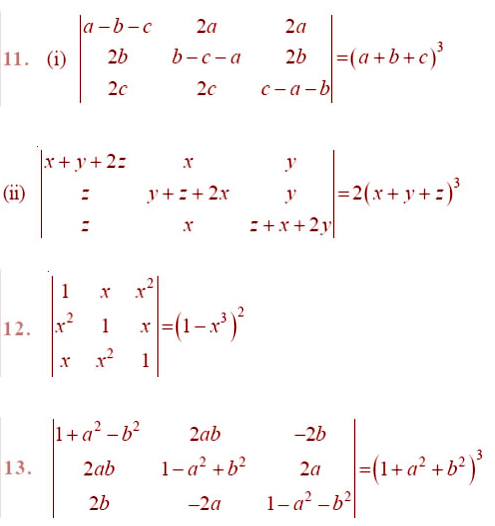
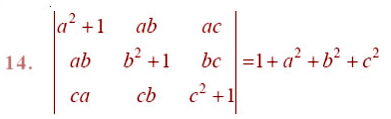
Question 15.Let A be a square matrix of order 3 × 3, then | kA| is equal to
(A) k| A|
(B) k2 | A|
(C) k3 | A|
(D) 3k | A |
Question 16. Which of the following is correct?
(A) Determinant is a square matrix.
(B) Determinant is a number associated to a matrix.
(C) Determinant is a number associated to a square matrix.
(D) None of these
Exercise
Question 1. Find area of the triangle with vertices at the point given in each of the following :
(i) (1, 0), (6, 0), (4, 3)
(ii) (2, 7), (1, 1), (10, 8)
(iii) (–2, –3), (3, 2), (–1, –8)
Question 2. Show that points A (a, b + c), B (b, c + a), C (c, a + b) are collinear.
Question 3. Find values of k if area of triangle is 4 sq.
units and vertices are
(i) (k, 0), (4, 0), (0, 2)
(ii) (–2, 0), (0, 4), (0, k)
Question 4.
(i) Find equation of line joining (1, 2) and (3, 6) using determinants.
(ii) Find equation of line joining (3, 1) and (9, 3) using determinants.
Question 5. If area of triangle is 35 sq units with vertices (2, – 6), (5, 4) and (k, 4). Then k is
(A) 12 (B) –2 (C) –12, –2 (D) 12, –2
Exercise
Write Minors and Cofactors of the elements of following determinants:

Exercise
=Find adjoint of each of the matrices in Exercises 1 and 2.
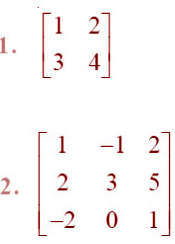
=Verify A (adj A) = (adj A) A = |A| I in Exercises 3 and 4
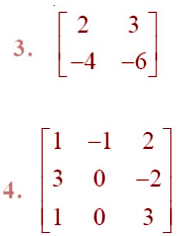
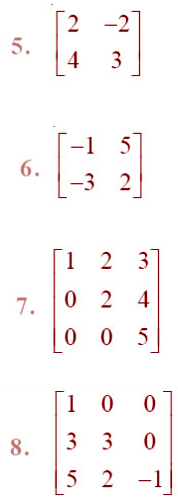
=Find the inverse of each of the matrices (if it exists) given in Exercises 5 to 11.


17. Let A be a nonsingular square matrix of order 3 × 3. Then |adj A| is equal to
(A) |A|
(B) |A|2
(C) |A|3
(D) 3|A|
18. If A is an invertible matrix of order 2, then det (A–1) is equal to
(A) det
(A) (B)1/det (A)
(C) 1
(D) 0
Exercise
Question 1. x + 2y = 2 and 2x + 3y = 3
Question 2. 2x – y = 5 and x + y = 4
Question 3. x + 3y = 5 and 2x + 6y = 8
Question 4. x + y + z = 1 , 2x + 3y + 2z = 2 and ax + ay + 2az = 4
Question 3x–y – 2z = 2, 2y – z =-1 and –3x – 5y = 3
Question 6. 5x – y + 4z = 5,2x + 3y + 5z = 2 and 5x – 2y + 6z = –1
Solve system of linear equations, using matrix method, in Exercises 7 to 14.
Question 7. 5x + 2y = 4 and 7x + 3y = 5
Question 8. 2x – y = –2 and 3x + 4y = 3
Question 9. 4x – 3y = 3 and 3x – 5y = 7
Question 10. 5x + 2y = 3 and 3x + 2y = 5
Question 11. 2x + y + z = 1, x – 2y – z =3/2 and 3y – 5z = 9
Question 12. x – y + z = 4, 2x + y – 3z = 0 and x + y + z = 2
Question 13. 2x + 3y +3 z = 5, x – 2y + z = – 4 and 3x – y – 2z = 3
Question 14. x – y + 2z = 7,3x + 4y – 5z = – 5 and 2x – y + 3z = 12
Question 15. If
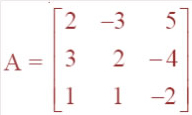 , find A–1. Using A–1 solve the system of equations 2x – 3y + 5z = 11 3x + 2y –
4z = – 5 x + y – 2z = – 3
, find A–1. Using A–1 solve the system of equations 2x – 3y + 5z = 11 3x + 2y –
4z = – 5 x + y – 2z = – 3
Question 16. The cost of 4 kg onion, 3 kg wheat and 2 kg rice is Rs 60. The cost of 2 kg onion, 4 kg wheat and 6 kg rice is Rs 90. The cost of 6 kg onion 2 kg wheat and 3 kg rice is Rs 70. Find cost of each item per kg by matrix method.
:: Chapter 6 - Application of Derivatives ::
EXERCISE
Question 1. Find the rate of change of the area of a circle with respect to its radius r when (a) r = 3 cm (b) r = 4 cm
Question 2. The volume of a cube is increasing at the rate of 8 cm3/s. How fast is the surface area increasing when the length of an edge is 12 cm?
Question 3. The radius of a circle is increasing uniformly at the rate of 3 cm/s. Find the rate at which the area of the circle is increasing when the radius is 10 cm.
Question 4. An edge of a variable cube is increasing at the rate of 3 cm/s. How fast is the volume of the cube increasing when the edge is 10 cm long?
Question 5. A stone is dropped into a quiet lake and waves move in circles at the speed of 5 cm/s. At the instant when the radius of the circular wave is 8 cm, how fast is the enclosed area increasing? 6. The radius of a circle is increasing at the rate of 0.7 cm/s. What is the rate of increase of its circumference?
Question 7. The length x of a rectangle is decreasing at the rate of 5 cm/minute and the width y is increasing at the rate of 4 cm/minute. When x = 8cm and y = 6cm, find the rates of change of (a) the perimeter, and (b) the area of the rectangle.
Question 8. A balloon, which always remains spherical on inflation, is being inflated by pumping in 900 cubic centimetres of gas per second. Find the rate at which the radius of the balloon increases when the radius is 15 cm.
Question 9. A balloon, which always remains spherical has a variable radius. Find the rate at which its volume is increasing with the radius when the later is 10 cm. 10. A ladder 5 m long is leaning against a wall. The bottom of the ladder is pulled along the ground, away from the wall, at the rate of 2cm/s. How fast is its height on the wall decreasing when the foot of the ladder is 4 m away from the wall
Question 11. A particle moves along the curve 6y = x3 +2. Find the points on the curve at which the y-coordinate is changing 8 times as fast as the x-coordinate.
Question 12. The radius of an air bubble is increasing at the rate of 1 2 cm/s. At what rate is the volume of the bubble increasing when the radius is 1 cm?
Question 13. A balloon, which always remains spherical, has a variable diameter 3 (2 1) 2 x + . Find the rate of change of its volume with respect to x.
Question 14. Sand is pouring from a pipe at the rate of 12 cm3/s. The falling sand forms a cone on the ground in such a way that the height of the cone is always one-sixth of the radius of the base. How fast is the height of the sand cone increasing when the height is 4 cm?
Question 15. The total cost C(x) in Rupees associated with the production of x units of an item is given by C(x) = 0.007x3 – 0.003x2 + 15x + 4000. Find the marginal cost when 17 units are produced.
Question 16. The total revenue in Rupees received from the sale of x units of a product is given by R(x) = 13x2 + 26x + 15. Find the marginal revenue when x = 7.
Question 17. The rate of change of the area of a circle with respect to its radius r at r = 6 cm is
(A) 10π
(B) 12π
(C) 8π
(D) 11π
Question 18. The total revenue in Rupees received from the sale of x units of a product is given by R(x) = 3x2 + 36x + 5. The marginal revenue, when x = 15 is
(A) 116
(B) 96
(C) 90
(D) 126
EXERCISE
Question 1. Show that the function given by f (x) = 3x + 17 is strictly increasing on R.
Question 2. Show that the function given by f (x) = e2x is strictly increasing on R.
Question 3. Show that the function given by f (x) = sin x is (a) strictly increasing in 0, 2 (b) strictly decreasing in , 2 (c) neither increasing nor decreasing in (0, π)
Question 4. Find the intervals in which the function f given by f (x) = 2x2 – 3x is (a) strictly increasing (b) strictly decreasing
Question 5. Find the intervals in which the function f given by f (x) = 2x3 – 3x2 – 36x + 7 is (a) strictly increasing (b) strictly decreasing
Question 6. Find the intervals in which the following functions are strictly increasing or decreasing:
(a) x2 + 2x – 5
(b) 10 – 6x – 2x2
(c) –2x3 – 9x2 – 12x + 1
(d) 6 – 9x – x2
(e) (x + 1)3 (x – 3)3
Question 7. Show that log(1 ) 2 2 y x x x = + −+ , x > – 1, is an increasing function of x throughout its domain.
Question 8. Find the values of x for which y = [x(x – 2)]2 is an increasing function.
Question 9. Prove that 4sin (2 cos ) y θ = −θ + θ is an increasing function of θ in 0, 2
Question 10. Prove that the logarithmic function is strictly increasing on (0, ∞).
Question 11. Prove that the function f given by f (x) = x2 – x + 1 is neither strictly increasing nor strictly decreasing on (– 1, 1)
Question 12. Which of the following functions are strictly decreasing on 0, 2?
(A) cos x
(B) cos 2x
(C) cos 3x
(D) tan x
Question 13. On which of the following intervals is the function f given by f (x) = x100 + sin x –1 strictly decreasing ? (A) (0,1) (B) , 2 (D) None of these
Question 14. Find the least value of a such that the function f given by f (x) = x2 + ax + 1 is strictly increasing on (1, 2).
Question 15. Let I be any interval disjoint from (–1, 1). Prove that the function f given by f (x) x 1 x = + is strictly increasing on I.
Question 16. Prove that the function f given by f (x) = log sin x is strictly increasing on 0, 2and strictly decreasing on .
Question 17. Prove that the function f given by f (x) = log cos x is strictly decreasing on 0, 2 ⎠ and strictly increasing on , 2 .
Question 18. Prove that the function given by f (x) = x3 – 3x2 + 3x – 100 is increasing in R.
Question 19. The interval in which y = x2 e–x is increasing is
(A) (– ∞, ∞)
(B) (– 2, 0)
(C) (2, ∞)
(D) (0, 2)
EXERCISE
Question 1. Find the slope of the tangent to the curve y = 3x4 – 4x at x = 4.
Question 2. Find the slope of the tangent to the curve 1, 2 2 y x x x − = ≠ − at x = 10.
Question 3. Find the slope of the tangent to curve y = x3 – x + 1 at the point whose x-coordinate is 2.
Question 4. Find the slope of the tangent to the curve y = x3 –3x + 2 at the point whose x-coordinate is 3.
Question 5. Find the slope of the normal to the curve x = acos3 θ, y = asin3 θ at . 4 π θ =
Question 6. Find the slope of the normal to the curve x = 1− asinθ, y = bcos2 θ at . 2 π θ =
Question 7. Find points at which the tangent to the curve y = x3 – 3x2 – 9x + 7 is parallel to the x-axis.
Question 8. Find a point on the curve y = (x – 2)2 at which the tangent is parallel to the chord joining the points (2, 0) and (4, 4).
Question 9. Find the point on the curve y = x3 – 11x + 5 at which the tangent is y = x – 11.
Question 10. Find the equation of all lines having slope – 1 that are tangents to the curve 1 1 y x = − , x ≠ 1.
Question 11. Find the equation of all lines having slope 2 which are tangents to the curve 1 3 y x = − , x ≠ 3.
Question 12. Find the equations of all lines having slope 0 which are tangent to the curve 2 1 . 2 3 y x x = − +
Question 13. Find points on the curve 2 2 1 9 16 x + y = at which the tangents are (i) parallel to x-axis (ii) parallel to y-axis.
Question 14. Find the equations of the tangent and normal to the given curves at the indicated points:
(i) y = x4 – 6x3 + 13x2 – 10x + 5 at (0, 5)
(ii) y = x4 – 6x3 + 13x2 – 10x + 5 at (1, 3)
(iii) y = x3 at (1, 1)
(iv) y = x2 at (0, 0)
(v) x = cos t, y = sin t at 4 t π =1
Question 15. Find the equation of the tangent line to the curve y = x2 – 2x +7 which is (a) parallel to the line 2x – y + 9 = 0 (b) perpendicular to the line 5y – 15x = 13.
Question 16. Show that the tangents to the curve y = 7x3 + 11 at the points where x = 2 and x = – 2 are parallel.
Question 17. Find the points on the curve y = x3 at which the slope of the tangent is equal to the y-coordinate of the point.
Question 18. For the curve y = 4x3 – 2x5, find all the points at which the tangent passes through the origin.
Question 19. Find the points on the curve x2 + y2 – 2x – 3 = 0 at which the tangents are parallel to the x-axis.
Question 20. Find the equation of the normal at the point (am2,am3) for the curve ay2 = x3.
Question 21. Find the equation of the normals to the curve y = x3 + 2x + 6 which are parallel to the line x + 14y + 4 = 0.
Question 22. Find the equations of the tangent and normal to the parabola y2 = 4ax at the point (at2, 2at).
Question 23. Prove that the curves x = y2 and xy = k cut at right angles* if 8k2 = 1.
Question 24. Find the equations of the tangent and normal to the hyperbola 2 2 2 2 1 x y a b − = at the point (x0, y0).
Question 25. Find the equation of the tangent to the curve y = 3x − 2 which is parallel to the line 4x − 2y + 5 = 0 . Choose the correct answer in Exercises 26 and 27.
Question 26. The slope of the normal to the curve y = 2x2 + 3 sin x at x = 0 is
(A) 3
(B) 1 3
(C) –3
(D) 1 3 −
Question 27. The line y = x + 1 is a tangent to the curve y2 = 4x at the point
(A) (1, 2)
(B) (2, 1)
(C) (1, – 2)
(D) (– 1, 2)
EXERCISE
Question 1. Using differentials, find the approximate value of each of the following up to 3 places of decimal.
(i) 25.3
(ii) 49.5
(iii) 0.6
(iv) 1 (0.009)3
(v) 1 (0.999)10
(vi) 1 (15)4
(vii) 1 (26)3
(viii) 1 (255)4
(ix) 1 (82)4
(x) 1 (401)2
(xi) 1 (0.0037)2
(xii) 1 (26.57)3
(xiii) 1 (81.5)4
(xiv) 3 (3.968)2
(xv) 1 (32.15)5
Question 2. Find the approximate value of f (2.01), where f (x) = 4x2 + 5x + 2.
Question 3. Find the approximate value of f (5.001), where f (x) = x3 – 7x2 + 15.
Question 4. Find the approximate change in the volume V of a cube of side x metres caused by increasing the side by 1%.
Question 5. Find the approximate change in the surface area of a cube of side x metres caused by decreasing the side by 1%.
Question 6. If the radius of a sphere is measured as 7 m with an error of 0.02 m, then find the approximate error in calculating its volume.
Question 7. If the radius of a sphere is measured as 9 m with an error of 0.03 m, then find the approximate error in calculating its surface area.
Question 8. If f(x) = 3x2 + 15x + 5, then the approximate value of f (3.02) is (A) 47.66 (B) 57.66 (C) 67.66 (D) 77.66 9. The approximate change in the volume of a cube of side x metres caused by increasing the side by 3% is
(A) 0.06 x3 m3
(B) 0.6 x3 m3
(C) 0.09 x3 m3
(D) 0.9 x3 m3
EXERCISE
Question 1. Find the maximum and minimum values, if any, of the following functions given by
(i) f
(x) = (2x – 1)2 + 3
(ii) f (x) = 9x2 + 12x + 2
(iii) f
(x) = –
(x – 1)2 + 10
(iv) g
(x) = x3 +
Question 1. It is given that at x = 1, the function x4 – 62x2 + ax + 9
attains its maximum value, on the interval [0, 2]. Find the value of a.
Question 2. Find the maximum and minimum values of x + sin 2x on [0, 2π].
Question 3. Find two numbers whose sum is 24 and whose product is as large as possible.
Question 4. Find two positive numbers x and y such that x + y = 60 and xy3 is maximum.
Question 5. Find two positive numbers x and y such that their sum is 35 and the product x2 y5 is a maximum.
Question 6. Find two positive numbers whose sum is 16 and the sum of whose cubes is minimum.
Question 7. A square piece of tin of side 18 cm is to be made into a box without top, by cutting a square from each corner and folding up the flaps to form the box. What should be the side of the square to be cut off so that the volume of the box is the maximum possible.
Question 8. A rectangular sheet of tin 45 cm by 24 cm is to be made into a box without top, by cutting off square from each corner and folding up the flaps. What should be the side of the square to be cut off so that the volume of the box is maximum ?
Question 9. Show that of all the rectangles inscribed in a given fixed circle, the square has the maximum area.
Question 10. Show that the right circular cylinder of given surface and maximum volume is such that its height is equal to the diameter of the base.
Question 11. Of all the closed cylindrical cans (right circular), of a given volume of 100 cubic centimetres, find the dimensions of the can which has the minimum surface area?
Question 12. A wire of length 28 m is to be cut into two pieces. One of the pieces is to be made into a square and the other into a circle. What should be the length of the two pieces so that the combined area of the square and the circle is minimum?
Question 13. Prove that the volume of the largest cone that can be inscribed in a sphere of radius R is 8 27 of the volume of the sphere.
Question 14. Show that the right circular cone of least curved surface and given volume has an altitude equal to 2 time the radius of the base.
Question 15. Show that the semi-vertical angle of the cone of the maximum volume and of given slant height is tan−1 2 .
Question 16. Show that semi-vertical angle of right circular cone of given surface area and maximum volume is sin 1 1
Miscellaneous Exercise on Chapter 6
Question 1. Using differentials, find the approximate value of each of the following: (a) 1 17 4 81 (b) ( ) 1 33 5 −
Question 2. Show that the function given by f (x) log x x = has maximum at x = e.
Question 3. The two equal sides of an isosceles triangle with fixed base b are decreasing at the rate of 3 cm per second. How fast is the area decreasing when the two equal sides are equal to the base
Question 4. Find the equation of the normal to curve x2 = 4y which passes through the point (1, 2).
Question 5. Show that the normal at any point θ to the curve x = a cosθ + a θ sin θ, y = a sinθ – aθ cosθ is at a constant distance from the origin.
Question 6. Find the intervals in which the function f given by ( ) 4sin 2 cos 2 cos f x x x x x x − − = + is
(i) increasing
(ii) decreasing.
Question 7. Find the intervals in which the function f given by 3 3 f (x) x 1 , x 0 x = + ≠ is
(i) increasing
(ii) decreasing.
Question 8. Find the maximum area of an isosceles triangle inscribed in the ellipse 2 2 2 2 1 x y a b + = with its vertex at one end of the major axis.
Question 9. A tank with rectangular base and rectangular sides, open at the top is to be constructed so that its depth is 2 m and volume is 8 m3. If building of tank costs Rs 70 per sq metres for the base and Rs 45 per square metre for sides. What is the cost of least expensive tank?
Question 10. The sum of the perimeter of a circle and square is k, where k is some constant. Prove that the sum of their areas is least when the side of square is double the radius of the circle.
Question 11. A window is in the form of a rectangle surmounted by a semicircular opening. The total perimeter of the window is
Question 12. m. Find the dimensions of the window to admit maximum light through the whole opening.
Question 13. A point on the hypotenuse of a triangle is at distance a and b from the sides of the triangle. Show that the maximum length of the hypotenuse is 2 2 3 (a3 + b3 )2 .
Question 14. Find the points at which the function f given by f (x) = (x – 2)4 (x + 1)3 has
(i) local maxima
(ii) local minima
(iii) point of inflexion
14. Find the absolute maximum and minimum values of the function f given by f (x) = cos2 x + sin x, x ∈ [0, π]
Question 15. Show that the altitude of the right circular cone of maximum volume that can be inscribed in a sphere of radius r is 4 3 r .
Question 16. Let f be a function defined on [a, b] such that f ′(x) > 0, for all x ∈ (a, b). Then prove that f is an increasing function on (a, b).
Question 17. Show that the height of the cylinder of maximum volume that can be inscribed in a sphere of radius R is 2R 3 . Also find the maximum volume.
Question 18. Show that height of the cylinder of greatest volume which can be inscribed in a right circular cone of height h and semi vertical angle α is one-third that of the cone and the greatest volume of cylinder is 4 3 tan2 27 πh α . Choose the correct answer in the Exercises from 19 to 24.
Question 19. A cylindrical tank of radius 10 m is being filled with wheat at the rate of 314 cubic metre per hour. Then the depth of the wheat is increasing at the rate of
(A) 1 m3/h
(B) 0.1 m3/h
(C) 1.1 m3/h
(D) 0.5 m3/h
Question 20. The slope of the tangent to the curve x = t2 + 3t – 8, y = 2t2 – 2t – 5 at the point (2,– 1) is
(A) 22 7
(B) 6 7
(C) 7 6
(D) 6 7
Question 21. The line y = mx + 1 is a tangent to the curve y2 = 4x if the value of m is
(A) 1
(B) 2
(C) 3
(D) 1 2
Question 22. The normal at the point (1,1) on the curve 2y + x2 = 3 is
(A) x + y = 0
(B) x – y = 0
(C) x + y +1 = 0
(D) x – y = 0
Question 23. The normal to the curve x2 = 4y passing (1,2) is
(A) x + y = 3
(B) x – y = 3
(C) x + y = 1
( D) x – y = 1
Question 24. The points on the curve 9y2 = x3, where the normal to the curve makes equal intercepts with the axes are
(A) 4, 8 3
(B) 4, 8 3
(C) 4, 3 8
(D) 4, 3 8
:: Chapter 7 - Integral ::
EXERCISE
Question 1. Find the area of the region bounded by the curve y2 = x and the lines x = 1, x = 4 and the x-axis.
Question 2. Find the area of the region bounded by y2 = 9x, x = 2, x = 4 and the x-axis in the first quadrant. Fig
Question 3. Find the area of the region bounded by x2 = 4y, y = 2, y = 4 and the y-axis in the first quadrant.
Question 4. Find the area of the region bounded by the ellipse 2 2 1 16 9 x y + = .
Question 5. Find the area of the region bounded by the ellipse 2 2 1 4 9 x y + = .
Question 6. Find the area of the region in the first quadrant enclosed by x-axis, line x = 3 y and the circle x2 + y2 = 4.
Question 7. Find the area of the smaller part of the circle x2 + y2 = a2 cut off by the line 2 x= a .
Question 8. The area between x = y2 and x = 4 is divided into two equal parts by the line x = a, find the value of a.
Question 9. Find the area of the region bounded by the parabola y = x2 and y = x .
Question 10. Find the area bounded by the curve x2 = 4y and the line x = 4y – 2.
Question 11. Find the area of the region bounded by the curve y2 = 4x and the line x = 3. Choose the correct answer in the following Exercises 12 and 13.
Question 12. Area lying in the first quadrant and bounded by the circle x2 + y2 = 4 and the lines x = 0 and x = 2 is
(A) π
(B) 2 π
(C) 3 π
(D) 4 π
Question 13. Area of the region bounded by the curve y2 = 4x, y-axis and the line y = 3 is
(A) 2
(B) 9 4
(C) 9 3
(D) 9 2
EXERCISE
Question 1. Find the area of the circle 4x2 + 4y2 = 9 which is interior to the parabola x2 = 4y.
Question 2. Find the area bounded by curves (x – 1)2 + y2 = 1 and x2 + y2 = 1.
Question 3. Find the area of the region bounded by the curves y = x2 + 2, y = x, x = 0 and x = 3.
Question 4. Using integration find the area of region bounded by the triangle whose vertices are (– 1, 0), (1, 3) and (3, 2).
Question 5. Using integration find the area of the triangular region whose sides have the equations y = 2x + 1, y = 3x + 1 and x =
Question 4.Choose the correct answer in the following exercises 6 and 7.
Question 6. Smaller area enclosed by the circle x2 + y2 = 4 and the line x + y = 2 is
(A) 2 (π – 2)
(B) π – 2
(C) 2π – 1
(D) 2 (π + 2)
Question 7. Area lying between the curves y2 = 4x and y = 2x is
(A) 2 3
(B) 1 3
(C) 1 4
(D) 3 4
Miscellaneous Exercise on Chapter
Question 1. Find the area under the given curves and given lines:
(i) y = x2, x = 1, x = 2 and x-axis
(ii) y = x4, x = 1, x = 5 and x-axis
Question 2. Find the area between the curves y = x and y = x2.
Question 3. Find the area of the region lying in the first quadrant and bounded by y = 4x2, x = 0, y = 1 and y = 4.
Question 4. Sketch the graph of y = x + 3 and evaluate 0 6 3 − ∫ x + dx .
Question 5. Find the area bounded by the curve y = sin x between x = 0 and x = 2π.
Question 6. Find the area enclosed between the parabola y2 = 4ax and the line y = mx.
Question 7. Find the area enclosed by the parabola 4y = 3x2 and the line 2y = 3x + 12.
Question 8. Find the area of the smaller region bounded by the ellipse 2 2 1 9 4 x + y = and the line 1 3 2 x y + = .
Question 9. Find the area of the smaller region bounded by the ellipse 2 2 2 2 x y 1 a b + = and the line 1 x y a b + = .
Question 10. Find the area of the region enclosed by the parabola x2 = y, the line y = x + 2 and the x-axis.
Question 11. Using the method of integration find the area bounded by the curve x + y = 1 . [Hint: The required region is bounded by lines x + y = 1, x– y = 1, – x + y = 1 and – x – y = 1].
Question 12. Find the area bounded by curves {(x, y) : y ≥ x2 and y = | x |}.
Question 13. Using the method of integration find the area of the triangle ABC, coordinates of whose vertices are A(2, 0), B (4, 5) and C (6, 3).
Question 14. Using the method of integration find the area of the region bounded by lines: 2x + y = 4, 3x – 2y = 6 and x – 3y + 5 = 0
Question 15. Find the area of the region {(x, y) : y2 ≤ 4x, 4x2 + 4y2 ≤ 9} Choose the correct answer in the following Exercises from 16 to 20.
Question 16. Area bounded by the curve y = x3, the x-axis and the ordinates x = – 2 and x = 1 is
(A) – 9
(B) 15 4 −
(C) 15 4
(D) 17 4
Question 17. The area bounded by the curve y = x | x | , x-axis and the ordinates x = – 1 and x = 1 is given by
(A) 0
(B) 1 3
(C) 2 3
(D) 4 3 [Hint : y = x2 if x > 0 and y = – x2 if x < 0].
Question 18. The area of the circle x2 + y2 = 16 exterior to the parabola y2 = 6x is
(A) 4 (4 3) 3 π −
(B) 4 (4 3) 3 π +
(C) 4 (8 3) 3 π −
(D) 4 (8 3) 3 π +
Question 19. The area bounded by the y-axis, y = cos x and y = sin x when 0 2 x π ≤ ≤ is
(A) 2 ( 2 −1)
(B) 2 −1
(C) 2 +1
(D) 2
:: Chapter 8 - Application Of Integrals ::
EXERCISE
1. Find the area of the region bounded by the curve y^2 =x and the lines x = 1 , x = 4 and the x axis
2.Find the area of the region bounded by y^2 = 9x, x=2, x =4 and the x axis in the first quadrant.
3. Find the area of the region bounded by x^2 = 4y, y = 2, y = 4 and the y-axis in the first quadrant.
Find the equation of the region bounded by the ellipse x^2/16 + y^2/9 =1
Find the equation of the region bounded by the ellipse x^2/4 + y^2/9 =1
6. find the area of the region in the first quadrant enclosed by x axis, line x =root 3 y and the circle x^2 + y^2 = 4
7.Area between x=y2 and x=4 is divided in two equal parts by the line x = a, find the value of a
8. The area between x^2 = y and x = 4 is divided into two equal parts by the line x = a, find the value of a.
9. Find the area of the region bounded by the parabola y = x^2 and y= |x|\
10. Find the area bounded by the curve x^2 =4y and the line x = 4y- 2
11. Find the area of the region bounded by the curve y2 = 4x and the line x = 3.
12. Area lying in the first quadrant and bounded by the circle x2 + y = 4 and the lines x = 0 and x = 2 is 2
13. Area of the region bounded by the curve y^2 =4x , y axis and the line y=3 is
EXERCISE
1. Find the area of the circle 4x^2 + 4y^2 = 9 which is interior to the parabola x^2 =4y
2. Find the area bounded by curves (x – 1)^2 + y^2 = 1 and x^2 + y^2 = 1
3.Find the area of the region bounded by the curves y= x^2 + 2 , y=x , x =0 and x = 3
4.Using integration find the area of region bounded by the triangle whose vertices are (– 1, 0), (1, 3) and (3, 2).
5. Using integration find the area of the triangular region whose sides have the equations y = 2x + 1, y = 3x + 1 and x = 4.
6. Smaller area enclosed by the circle x^2 +y^2 = 4 and the lines x + y = 2 is (A) 2 (π – 2) (B) π – 2 (C) 2π – 1 (D) 2 (π + 2)
7. Area lying between the curves y^2 = 4x and y = 2x is
Miscellaneous Solutions
1. Find the area under the given curves and given lines (i) y = x^2 , x=1 , x= 2 and x axis (ii) y = x^4 , x=1 , x= 5 and x axis
2. Find the area between the curves y = x and y = x^2
3.Find the area of the region lying in the first quadrant and bounded by y = 4x^2, x=0, y=1 and y= 4
4. Sketch the graph of y = x + 3 and evaluate integration limits 6 to 0 of x + 3 dx
5. Find the area bounded by the curve y = sin x between x = 0 and x = 2π.
6. Find the area enclosed between the parabola y^2 = 4ax and the line y =mx
7. Find the area enclosed by the parabola 4y = 3x^2 and the line 2y = 3x + 12 using integration to find area,
8. Find the area of the smaller region bounded by the ellipse x^2/9 + y^2/4 = 1 and the line x/3 + y/2 =1
:: Chapter 9 - Differential Equations ::

EXERCISE 9.2
In each of the Exercises 1 to 10 verify that the given functions (explicit or
implicit) is a solution of the corresponding differential equation:
Question 1. y = ex + 1 : y″ – y′ = 0
Question 2. y = x2 + 2x + C : y′ – 2x – 2 = 0
Question 3. y = cos x + C : y′ + sin x = 0
Question 4. y = 1+ x2 : y′ = 1 2 xy + x
Question 5. y = Ax : xy′ = y (x ≠ 0)
Question 6. y = x sin x : xy′ = y + x x2 − y2 (x ≠ 0 and x
> y or x < – y)
Question 7. xy = log y + C : y′ = 2 1 y − xy (xy ≠ 1)
Question 8. y – cos y = x : (y sin y + cos y + x) y′ = y
Question 9. x + y = tan–1y : y2 y′ + y2 + 1 = 0
Question 10. y = a2
− x2 x ∈ (–a, a) : x + y dy dx = 0 (y ≠ 0)
Question 11. The number of arbitrary constants in the general solution of a
differential equation of fourth order are:
(A) 0
(B) 2
(C) 3
(D) 4
Question 12. The number of arbitrary constants in the particular solution of a
differential equation of third order are:
(A) 3
(B) 2
(C) 1
(D) 0
EXERCISE 9.3
In each of the Exercises 1 to 5, form a differential equation representing
the given family of curves by eliminating arbitrary constants a and b.
Question 1. x y 1 a b + =
Question 2. y2 = a (b2 – x2)
Question 3. y = a e3x + b e– 2x
Question 4. y = e2x (a + bx)
Question 5. y = ex (a cos x + b sin x)
Question 6. Form the differential equation of the family of circles touching the
y-axis at origin.
Question 7. Form the differential equation of the family of parabolas having
vertex at origin and axis along positive y-axis.
Question 8. Form the differential equation of the family of ellipses having foci
on y-axis and centre at origin.
Question 9. Form the differential equation of the family of hyperbolas having
foci on x-axis and centre at origin.
Question 10. Form the differential equation of the family of circles having
centre on y-axis and radius 3 units.
Question 11. Which of the following differential equations has y = c1 ex + c2
e–x as the general solution?
(A) 2 2 d y y 0 dx + =
(B) 2 2 d y y 0 dx − =
(C) 2 2 d y 1 0 dx + =
(D) 2 2 d y 1 0 dx − =
Question 12. Which of the following differential equations has y = x as one
of its particular solution?
(A) 2 2 2 d y x dy xy x dx dx − + =
(B) 2 2 d y x dy xy x dx dx + + =
(C) 2 2 2 d y x dy xy 0 dx dx − + =
(D) 2 2 d y x dy xy 0 dx dx |
EXERCISE 9.4
EXERCISE 9.3
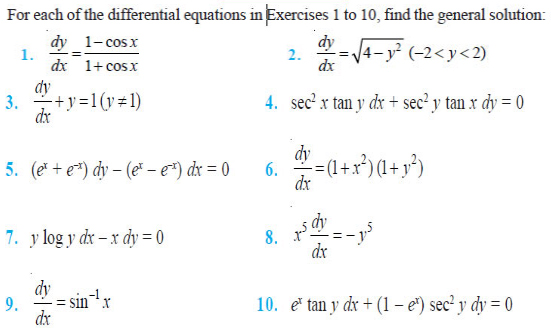

Question 17. Find the equation of a curve passing through the
point (0, –2) given that at any point (x, y) on the curve, the product of the
slope of its tangent and y coordinate of the point is equal to the x coordinate
of the point.
Question 18. At any point (x, y) of a curve, the slope of the tangent is twice
the slope of the line segment joining the point of contact to the point (– 4,
–3). Find the equation of the curve given that it passes through (–2, 1).
Question 19. The volume of spherical balloon being inflated changes at a
constant rate. If initially its radius is 3 units and after 3 seconds it is 6
units. Find the radius of balloon after t seconds.
Question 20. In a bank, principal increases continuously at the rate of r% per
year. Find the value of r if Rs 100 double itself in 10 years (loge2 = 0.6931).
Question 21. In a bank, principal increases continuously at the rate of 5% per
year. An amount of Rs 1000 is deposited with this bank, how much will it worth
after 10 years (e0.5 = 1.648).
Question 22. In a culture, the bacteria count is 1,00,000. The number is
increased by 10% in 2 hours. In how many hours will the count reach 2,00,000, if
the rate of growth of bacteria is proportional to the number present?
Question 23. The general solution of the differential equation dy ex y dx = + is
(A) ex + e–y = C (B) ex + ey = C (C) e–x + ey = C (D) e–x + e–y = C

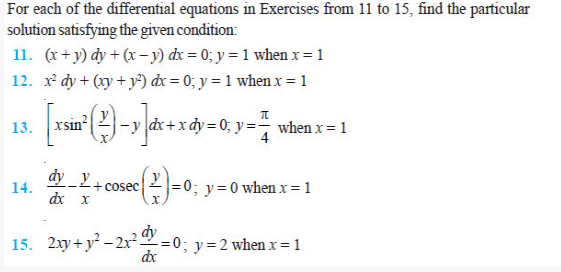
Question 16. A homogeneous differential equation of the from
dx h x dy y = can be solved by making the substitution.
(A) y = vx
(B) v = yx
(C) x = vy
(D) x = v
Question 17. Which of the following is a homogeneous differential equation?
(A) (4x + 6y + 5) dy – (3y + 2x + 4) dx = 0
(B) (xy) dx – (x3 + y3) dy = 0
(C) (x3 + 2y2) dx + 2xy dy = 0
(D) y2 dx + (x2 – xy – y2) dy = 0


Miscellaneous Exercise on Chapter 9
Question 1. For each of the differential equations given
below, indicate its order and degree (if defined).
(i) 2 2 2 d y 5x dy 6y log x dx dx +
(ii) 3 2 dy 4 dy 7 y sin x dx dx
(iii) 4 3 4 3 d y sin d y 0 dx dx
Question 2. For each of the exercises given below, verify that the given
function (implicit or explicit) is a solution of the corresponding differential
equation.
(i) y = a ex + b e–x + x2 : 2 2 2 x d y 2 dy xy x 2 0 dx dx + − + − =
(ii) y = ex (a cos x + b sin x) : 2 2 d y 2 dy 2y 0 dx dx − + =
(iii) y = x sin 3x : 2 2 d y 9y 6cos3x 0 dx + − =
(iv) x2 = 2y2 log y : (x2 y2 ) dy xy 0 dx + − =
Question 3. Form the differential equation representing the family of curves
given by (x – a)2 + 2y2 = a2, where a is an arbitrary constant.
Question 4. Prove that x2 – y2 = c (x2 + y2)2 is the general solution of
differential equation (x3 – 3x y2) dx = (y3 – 3x2y) dy, where c is a parameter.
Question 5. Form the differential equation of the family of circles in the first
quadrant which touch the coordinate axes.
Question 6. Find the general solution of the differential equation 2 2 1 0 1 dy
y dx x − + = − .
Question 7. Show that the general solution of the differential equation 2 2 1 0
1 dy y y dx x x + + + = + + is given by (x + y + 1) = A (1 – x – y – 2xy), where
A is parameter.
Question 8. Find the equation of the curve passing through the point 0, 4 whose
differential equation is sin x cos y dx + cos x sin y dy = 0.
Question 9. Find the particular solution of the differential equation (1 + e2x)
dy + (1 + y2) ex dx = 0, given that y = 1 when x = 0.
Question 10. Solve the differential equation 2 ( 0) x x y e ydx x e y y dy y ≠ .
Question 11. Find a particular solution of the differential equation (x – y) (dx
+ dy) = dx – dy, given that y = –1, when x = 0. (Hint: put x – y = t)
Question 12. Solve the differential equation 2 1( 0) x e y dxx x x dy.
Question 13. Find a particular solution of the differential equation cot dy y x
dx + = 4x cosec x (x ≠ 0), given that y = 0 when 2 x π = .
Question 14. Find a particular solution of the differential equation (x + 1) dy
dx = 2 e–y – 1, given that y = 0 when x = 0.
Question 15. The population of a village increases continuously at the rate
proportional to the number of its inhabitants present at any time. If the
population of the village was 20, 000 in 1999 and 25000 in the year 2004, what
will be the population of the village in 2009?
Question 16. The general solution of the differential equation y dx x dy 0 y
− = is
(A) xy = C
(B) x = Cy2
(C) y = Cx
(D) y = Cx2
Question 17. The general solution of a differential equation of the type P1
Q1 dx x dy + = is
(A) P1 ( P1 ) Q1 C dy dy y e∫ = ∫ e∫ dy +
(B) P1 ( P1 ) . Q1 C dx dx y e∫ = ∫ e∫ dx +
(C) P1 ( P1 ) Q1 C dy dy x e∫ = ∫ e∫ dy +
(D) P1 ( P1 ) Q1 C dx dx x e∫ = ∫ e∫ dx +
Question 18. The general solution of the differential equation ex dy + (y ex
+ 2x) dx = 0 is
(A) x ey + x2 = C
(B) x ey + y2 = C
(C) y ex + x2 = C
(D) y ey + x2 = C
:: Chapter 10 - Vector Algebra ::
Question 1. Represent graphically a displacement of 40 km,
30° east of north.
Question 2. Classify the following measures as scalars and vectors.
(i) 10 kg
(ii) 2 meters north-west
(iii) 40° (iv) 40 watt
(v) 10–19 coulomb
(vi) 20 m/s2
Question 3. Classify the following as scalar and vector quantities.
(i) time period
(ii) distance
(iii) force
(iv) velocity
(v) work done
Question 4. In Fig 10.6 (a square), identify the following vectors.
(i) Coinitial
(ii) Equal
(iii) Collinear but not equal
Question 5. Answer the following as true or false.
(i) a and −a are collin ear.
(ii) Two collinear vectors are always equal in magnitude.
(iii) Two vectors having same magnitude are collinear.
(iv) Two collinear vectors having the same magnitude are equal.
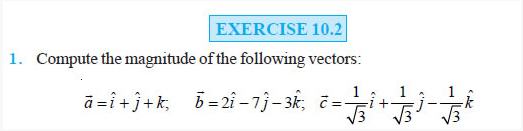
Question 2. Write two different vectors having same magnitude.
Question 3. Write two different vectors having same direction.
Question 4. Find the values of x and y so that the vectors 2iˆ + 3 ˆj and xiˆ +
yˆj are equal.
Question 5. Find the scalar and vector components of the vector with initial
point (2, 1) and terminal point (– 5, 7).
Question 6. Find the sum of the vectors a = iˆ − 2 ˆj + kˆ, b = −2iˆ + 4 ˆj +
5kˆ and c� = iˆ − 6 ˆj – 7kˆ .
Question 7. Find the unit vector in the direction of the vector a = iˆ + ˆj +
2kˆ .
Question 8. Find the unit vector in the direction of vector PQ, where P and Q
are the points (1, 2, 3) and (4, 5, 6), respectively.
Question 9. For given vectors, a = 2iˆ − ˆj + 2kˆ and b = −iˆ + ˆj − kˆ , find
the unit vector in the direction of the vector a + b .
Question 10. Find a vector in the direction of vector 5iˆ − ˆj + 2kˆ which has
magnitude 8 units.
Question 11. Show that the vectors 2iˆ − 3 ˆj + 4kˆ and − 4iˆ + 6 ˆj − 8kˆ are
collinear. 12. Find the direction cosines of the vector iˆ + 2 ˆj + 3kˆ .
Question 13. Find the direction cosines of the vector joining the points A(1, 2,
–3) and B(–1, –2, 1), directed from A to B .
Question 14. Show that the vector iˆ + ˆj + kˆ is equally inclined to the axes
OX, OY and OZ.
Question 15. Find the position vector of a point R which divides the line
joining two points P and Q whose position vectors are iˆ + 2 ˆj − kˆ and – iˆ +
ˆj + kˆ respectively, in the ratio 2 : 1
(i) internally
(ii) externally






:: Chapter 11 - Three Dimensional Geometry ::
EXERCISE 11.1
Question 1. If a line makes angles 90°, 135°, 45° with the x, y
and z-axes respectively, find its direction cosines.
Question 2. Find the direction cosines of a line which makes equal angles with
the coordinate axes.
Question 3. If a line has the direction ratios –18, 12, – 4,
then what are its direction cosines ?
Question 4. Show that the points (2, 3, 4), (– 1, – 2, 1), (5, 8, 7) are
collinear.
Question 5. Find the direction cosines of the sides of the triangle whose
vertices are (3, 5, – 4), (– 1, 1, 2) and (– 5, – 5, – 2).
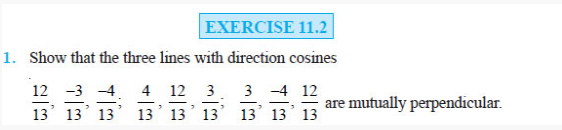
Question 2. Show that the line through the points (1, – 1, 2),
(3, 4, – 2) is perpendicular to the line through the points (0, 3, 2) and (3, 5,
6).
Question 3. Show that the line through the points (4, 7, 8), (2, 3, 4) is
parallel to the line through the points (– 1, – 2, 1), (1, 2, 5).
Question 4. Find the equation of the line which passes through the point (1, 2,
3) and is parallel to the vector 3 iˆ + 2 ˆj −2 kˆ .
Question 5. Find the equation of the line in vector and in cartesian form that
passes through the point with position vector 2 iˆ− j + 4 kˆ and is in the
direction iˆ + 2 ˆj − kˆ .
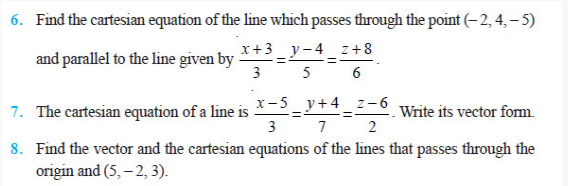
Question 9. Find the vector and the cartesian equations of the
line that passes through the points (3, – 2, – 5), (3, – 2, 6).
Question 10. Find the angle between the following pairs of lines:
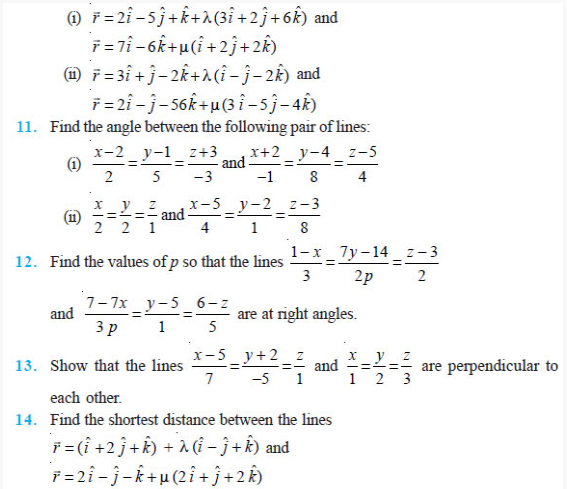

EXERCISE 11.3
Question 1. In each of the following cases, determine the
direction cosines of the normal to the plane and the distance from the origin.
(a) z = 2
(b) x + y + z = 1
(c) 2x + 3y – z = 5
(d) 5y + 8 = 0
Question 2. Find the vector equation of a plane which is at a distance of 7
units from the origin and normal to the vector 3 iˆ + 5 ˆj − 6 kˆ.
Question 3. Find the Cartesian equation of the following planes:
(a) r (iˆ + ˆj − kˆ) = 2
(b) r (2iˆ +3 ˆj − 4kˆ) = 1
(c) r [(s − 2t) iˆ + (3 − t) ˆj +(2 s +t ) kˆ] = 15
Question 4. In the following cases, find the coordinates of the foot of the
perpendicular drawn from the origin.
(a) 2x + 3y + 4z – 12 = 0 (b) 3y + 4z – 6 = 0
(c) x + y + z = 1 (d) 5y + 8 = 0
Question 5. Find the vector and cartesian equations of the planes
(a) that passes through the point (1, 0, – 2) and the normal to the plane is
iˆ + ˆj − kˆ.
(b) that passes through the point (1,4, 6) and the normal vector to the plane is
iˆ−2 ˆj + kˆ.
Question 6. Find the equations of the planes that passes through three
points.
(a) (1, 1, – 1), (6, 4, – 5), (– 4, – 2, 3)
(b) (1, 1, 0), (1, 2, 1), (– 2, 2, – 1)
Question 7. Find the intercepts cut off by the plane 2x + y – z = 5.
Question 8. Find the equation of the plane with intercept 3 on the y-axis and
parallel to ZOX plane.
Question 9. Find the equation of the plane through the intersection of the
planes 3x – y + 2z – 4 = 0 and x + y + z – 2 = 0 and the point (2, 2, 1).
Question 10. Find the vector equation of the plane passing through the
intersection of the planes r .(2 iˆ + 2 ˆj − 3 kˆ ) = 7 , r .(2 iˆ + 5 ˆj + 3 kˆ
) = 9 and through the point (2, 1, 3).
Question 11. Find the equation of the plane through the line of intersection of
the planes x + y + z = 1 and 2x + 3y + 4z = 5 which is perpendicular to the
plane x – y + z = 0.
Question 12. Find the angle between the planes whose vector equations are r (2 iˆ
+ 2 ˆj − 3 kˆ) = 5 and r (3 iˆ − 3 ˆj + 5 kˆ) = 3 .
Question 13. In the following cases, determine whether the given planes are
parallel or perpendicular, and in case they are neither, find the angles between
them.
(a) 7x + 5y + 6z + 30 = 0 and 3x – y – 10z + 4 = 0
(b) 2x + y + 3z – 2 = 0 and x – 2y + 5 = 0
(c) 2x – 2y + 4z + 5 = 0 and 3x – 3y + 6z – 1 = 0
(d) 2x – y + 3z – 1 = 0 and 2x – y + 3z + 3 = 0
(e) 4x + 8y + z – 8 = 0 and y + z – 4 = 0
Question 14. In the following cases, find the distance of each of the given
points from the corresponding given plane.
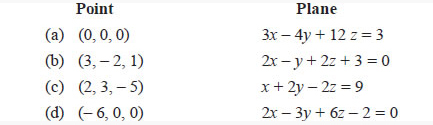
Miscellaneous Exercise on Chapter 11
Question 1. Show that the line joining the origin to the point
(2, 1, 1) is perpendicular to the line determined by the points (3, 5, – 1), (4,
3, – 1).
Question 2. If l1, m1, n1 and l2, m2, n2 are the direction cosines of two
mutually perpendicular lines, show that the direction cosines of the line
perpendicular to both of these are 1 2 2 1 1 2 2 1 1 2 2 1 m n − m n , n l − n l
, l m − l m
Question 3. Find the angle between the lines whose direction ratios are a, b, c
and b – c, c – a, a – b.
Question 4. Find the equation of a line parallel to x-axis and passing through
the origin.
Question 5. If the coordinates of the points A, B, C, D be (1, 2, 3), (4, 5, 7),
(– 4, 3, – 6) and (2, 9, 2) respectively, then find the angle between the lines
AB and CD.

Question 10. Find the coordinates of the point where the line
through (5, 1, 6) and (3, 4,1) crosses the YZ-plane.
Question 11. Find the coordinates of the point where the line through (5, 1, 6)
and (3, 4, 1) crosses the ZX-plane.
Question 12. Find the coordinates of the point where the line through (3, – 4, –
5) and (2, – 3, 1) crosses the plane 2x + y + z = 7.
Question 13. Find the equation of the plane passing through the point (– 1, 3,
2) and perpendicular to each of the planes x + 2y + 3z = 5 and 3x + 3y + z = 0.
Question 14. If the points (1, 1, p) and (– 3, 0, 1) be equidistant from the
plane (3 ˆ + 4 ˆ −12 ˆ) +13 = 0, r i j k then find the value of p.
Question 15. Find the equation of the plane passing through the line of
intersection of the planes r (iˆ + ˆj + kˆ) =1 and r (2 iˆ + 3 ˆj − kˆ) + 4 = 0
and parallel to x-axis.
Question 16. If O be the origin and the coordinates of P be (1, 2, – 3), then
find the equation of the plane passing through P and perpendicular to OP.
Question 17. Find the equation of the plane which contains the line of
intersection of the planes r (iˆ + 2 ˆj + 3 kˆ) − 4 = 0 , r (2 iˆ + ˆj − kˆ) + 5
= 0 and which is perpendicular to the plane r (5 iˆ + 3 ˆj − 6kˆ) + 8 = 0 ] .
Question 18. Find the distance of the point (– 1, – 5, – 10) from the point of
intersection of the line r = 2 iˆ − ˆj + 2 kˆ + λ (3 iˆ + 4 ˆj + 2 kˆ) and the
plane r (iˆ − ˆj + kˆ) = 5 .
Question 19. Find the vector equation of the line passing through (1, 2, 3) and
parallel to the planes r (iˆ − ˆj + 2kˆ) = 5 and r (3 iˆ + ˆj + kˆ) = 6 .
Question 20. Find the vector equation of the line passing through the point (1,
2, – 4) and perpendicular to the two lines:

:: Chapter 12 - Linear Programming ::
EXERCISE 12.1
Solve the following Linear Programming Problems
graphically:
Question 1. Maximise Z = 3x + 4y subject to the constraints : x + y ≤ 4, x ≥ 0,
y ≥ 0.
Question 2. Minimise Z = – 3x + 4 y subject to x + 2y ≤ 8, 3x + 2y ≤ 12, x ≥ 0,
y ≥ 0.
Question 3. Maximise Z = 5x + 3y subject to 3x + 5y ≤ 15, 5x + 2y ≤ 10, x ≥ 0, y
≥ 0.
Question 4. Minimise Z = 3x + 5y such that x + 3y ≥ 3, x + y ≥ 2, x, y ≥ 0.
Question 5. Maximise Z = 3x + 2y subject to x + 2y ≤ 10, 3x + y ≤ 15, x, y ≥ 0.
Question 6. Minimise Z = x + 2y subject to 2x + y ≥ 3, x + 2y ≥ 6, x, y ≥ 0.
Show that the minimum of Z occurs at more than two points.
Question 7. Minimise and Maximise Z = 5x + 10 y subject to x + 2y ≤ 120, x + y ≥
60, x – 2y ≥ 0, x, y ≥ 0.
Question 8. Minimise and Maximise Z = x + 2y subject to x + 2y ≥ 100, 2x – y ≤
0, 2x + y ≤ 200; x, y ≥ 0.
Question 9. Maximise Z = – x + 2y, subject to the constraints: x ≥ 3, x + y ≥ 5,
x + 2y ≥ 6, y ≥ 0.
Question 10. Maximise Z = x + y, subject to x – y ≤ –1, –x + y ≤ 0, x, y ≥ 0.
EXERCISE 12.2
Question 1. Reshma wishes to mix two types of food P and Q in
such a way that the vitamin contents of the mixture contain at least 8 units of
vitamin A and 11 units of vitamin B. Food P costs Rs 60/kg and Food Q costs Rs
80/kg. Food P contains 3 units/kg of Vitamin A and 5 units / kg of Vitamin B
while food Q contains 4 units/kg of Vitamin A and 2 units/kg of vitamin B.
Determine the minimum cost of the mixture.
Question 2. One kind of cake requires 200g of flour and 25g of fat, and another
kind of cake requires 100g of flour and 50g of fat. Find the maximum number of
cakes which can be made from 5kg of flour and 1 kg of fat assuming that there is
no shortage of the other ingredients used in making the cakes.
Question 3. A factory makes tennis rackets and cricket bats. A tennis racket
takes 1.5 hours of machine time and 3 hours of craftman’s time in its making
while a cricket bat takes 3 hour of machine time and 1 hour of craftman’s time.
In a day, the factory has the availability of not more than 42 hours of machine
time and 24 hours of craftsman’s time.
(i) What number of rackets and bats must be made if the factory is to work at
full capacity?
(ii) If the profit on a racket and on a bat is Rs 20 and Rs 10 respectively,
find the maximum profit of the factory when it works at full capacity.
Question 4. A manufacturer produces nuts and bolts. It takes 1 hour of work on
machine A and 3 hours on machine B to produce a package of nuts. It takes 3
hours on machine A and 1 hour on machine B to produce a package of bolts. He
earns a profit of Rs17.50 per package on nuts and Rs 7.00 per package on bolts.
How many packages of each should be produced each day so as to maximise his
profit, if he operates his machines for at the most 12 hours a day?
Question 5. A factory manufactures two types of screws, A and B. Each type of
screw requires the use of two machines, an automatic and a hand operated. It
takes 4 minutes on the automatic and 6 minutes on hand operated machines to
manufacture a package of screws A, while it takes 6 minutes on automatic and 3
minutes on the hand operated machines to manufacture a package of screws B. Each
machine is available for at the most 4 hours on any day. The manufacturer can
sell a package of screws A at a profit of Rs 7 and screws B at a profit of Rs
10. Assuming that he can sell all the screws he manufactures, how many packages
of each type should the factory owner produce in a day in order to maximise his
profit? Determine the maximum profit.
Question 6. A cottage industry manufactures pedestal lamps and wooden shades,
each requiring the use of a grinding/cutting machine and a sprayer. It takes 2
hours on grinding/cutting machine and 3 hours on the sprayer to manufacture a
pedestal lamp. It takes 1 hour on the grinding/cutting machine and 2 hours on
the sprayer to manufacture a shade. On any day, the sprayer is available for at
the most 20 hours and the grinding/cutting machine for at the most 12 hours. The
profit from the sale of a lamp is Rs 5 and that from a shade is Rs 3. Assuming
that the manufacturer can sell all the lamps and shades that he produces, how
should he schedule his daily production in order to maximise his profit?
Question 7. A company manufactures two types of novelty souvenirs made of
plywood. Souvenirs of type A require 5 minutes each for cutting and 10 minutes
each for assembling. Souvenirs of type B require 8 minutes each for cutting and
8 minutes each for assembling. There are 3 hours 20 minutes available for
cutting and 4 hours for assembling. The profit is Rs 5 each for type A and Rs 6
each for type B souvenirs. How many souvenirs of each type should the company
manufacture in order to maximise the profit?
Question 8. A merchant plans to sell two types of personal computers – a desktop
model and a portable model that will cost Rs 25000 and Rs 40000 respectively. He
estimates that the total monthly demand of computers will not exceed 250 units.
Determine the number of units of each type of computers which the merchant
should stock to get maximum profit if he does not want to invest more than Rs 70
lakhs and if his profit on the desktop model is Rs 4500 and on portable model is
Rs 5000.
Question 9. A diet is to contain at least 80 units of vitamin A and 100 units of
minerals. Two foods F1 and F2 are available. Food F1 costs Rs 4 per unit food
and F2 costs Rs 6 per unit. One unit of food F1 contains 3 units of vitamin A
and 4 units of minerals. One unit of food F2 contains 6 units of vitamin A and 3
units of minerals. Formulate this as a linear programming problem. Find the
minimum cost for diet that consists of mixture of these two foods and also meets
the minimal nutritional requirements.
Question 10. There are two types of fertilisers F1 and F2. F1 consists of 10%
nitrogen and 6% phosphoric acid and F2 consists of 5% nitrogen and 10%
phosphoric acid. After testing the soil conditions, a farmer finds that she
needs atleast 14 kg of nitrogen and 14 kg of phosphoric acid for her crop. If F1
costs Rs 6/kg and F2 costs Rs 5/kg, determine how much of each type of
fertiliser should be used so that nutrient requirements are met at a minimum
cost. What is the minimum cost?
Question 11. The corner points of the feasible region determined by the
following system of linear inequalities: 2x + y ≤ 10, x + 3y ≤ 15, x, y ≥ 0 are
(0, 0), (5, 0), (3, 4) and (0, 5). Let Z = px + qy, where p, q > 0. Condition on
p and q so that the maximum of Z occurs at both (3, 4) and (0, 5) is
(A) p = q
(B) p = 2q
(C) p = 3q
(D) q = 3p
Miscellaneous Exercise
Question 1. Refer to Example 9. How many packets of each food
should be used to maximise the amount of vitamin A in the diet? What is the
maximum amount of vitamin A
Question 2. A farmer mixes two brands P and Q of cattle feed. Brand P, costing
Rs 250 per bag, contains 3 units of nutritional element A, 2.5 units of element
B and 2 units of element C. Brand Q costing Rs 200 per bag contains 1.5 units of
nutritional element A, 11.25 units of element B, and 3 units of element C. The
minimum requirements of nutrients A, B and C are 18 units, 45 units and 24 units
respectively. Determine the number of bags of each brand which should be mixed
in order to produce a mixture having a minimum cost per bag? What is the minimum
cost of the mixture per bag?
Question 3. A dietician wishes to mix together two kinds of food X and Y in such
a way that the mixture contains at least 10 units of vitamin A, 12 units of
vitamin B and 8 units of vitamin C. The vitamin contents of one kg food is given
below: in the diet?
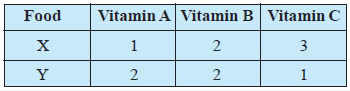
One kg of food X costs Rs 16 and one kg of food Y costs Rs
Question 20. Find the least cost of the mixture which will produce the required
diet? 4. A manufacturer makes two types of toys A and B. Three machines are
needed for this purpose and the time (in minutes) required for each toy on the
machines is given below:
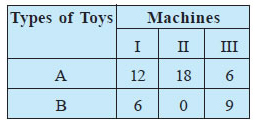
Each machine is available for a maximum of 6 hours per day. If the profit on each toy of type A is Rs 7.50 and that on each toy of type B is Rs 5, show that 15 toys of type A and 30 of type B should be manufactured in a day to get maximum profit.
Question 5. An aeroplane can carry a maximum of 200 passengers. A profit of Rs 1000 is made on each executive class ticket and a profit of Rs 600 is made on each economy class ticket. The airline reserves at least 20 seats for executive class. However, at least 4 times as many passengers prefer to travel by economy class than by the executive class. Determine how many tickets of each type must be sold in order to maximise the profit for the airline. What is the maximum profit?
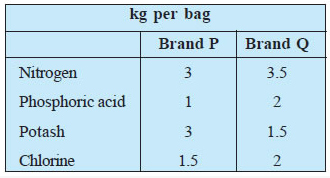
Question 9. Refer to Question 8. If the grower wants to maximise the amount of nitrogen added to the garden, how many bags of each brand should be added? What is the maximum amount of nitrogen added?
Question 10. A toy company manufactures two types of dolls, A and B. Market tests and available resources have indicated that the combined production level should not exceed 1200 dolls per week and the demand for dolls of type B is at most half of that for dolls of type A. Further, the production level of dolls of type A can exceed three times the production of dolls of other type by at most 600 units. If the company makes profit of Rs 12 and Rs 16 per doll respectively on dolls A and B, how many of each should be produced weekly in order to maximise the profit?
:: Chapter 13 - Probability ::

Question 7. Two coins are tossed once, where (i) E : tail appears on one
coin, F : one coin shows head (ii) E : no tail appears, F : no head appears
Question 8. A die is thrown three times, E : 4 appears on the third toss, F : 6
and 5 appears respectively on first two tosses
Question 9. Mother, father and son line up at random for a family picture E :
son on one end, F : father in middle
Question 10. A black and a red dice are rolled.
(a) Find the conditional probability of obtaining a sum greater than 9,
given that the black die resulted in a 5 .
(b) Find the conditional probability of obtaining the sum 8, given that the red
die resulted in a number less than 4.
Question 11. A fair die is rolled. Consider events E = {1,3,5}, F = {2,3} and
G = {2,3,4,5} Find
(i) P(E|F) and P(F|E)
(ii) P(E|G) and P(G|E)
(iii) P((E ∪ F)|G) and P ((E ∩ F)|G)
Question 12. Assume that each born child is equally likely to be a boy or a
girl. If a family has two children, what is the conditional probability that
both are girls given that (i) the youngest is a girl, (ii) at least one is a
girl?
Question 13. An instructor has a question bank consisting of 300 easy True /
False questions, 200 difficult True / False questions, 500 easy multiple choice
questions and 400 difficult multiple choice questions. If a question is selected
at random from the question bank, what is the probability that it will be an
easy question given that it is a multiple choice question?
Question 14. Given that the two numbers appearing on throwing two dice are
different. Find the probability of the event ‘the sum of numbers on the dice is
4’.
Question 15. Consider the experiment of throwing a die, if a multiple of 3 comes
up, throw the die again and if any other number comes, toss a coin. Find the
conditional probability of the event ‘the coin shows a tail’, given that ‘at
least one die shows a 3’. In each of the Exercises 16 and 17 choose the correct
answer:
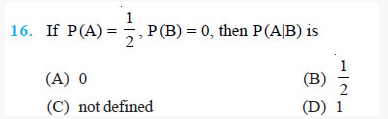
Question 17. If A and B are events such that P(A|B) = P(B|A), then (
A) A ⊂ B but A ≠ B
(B) A = B
(C) A ∩ B = φ
(D) P(A) = P(B)

Question 2. Two cards are drawn at random and without replacement from a pack
of 52 playing cards. Find the probability that both the cards are black.
Question 3. A box of oranges is inspected by examining three randomly selected
oranges drawn without replacement. If all the three oranges are good, the box is
approved for sale, otherwise, it is rejected. Find the probability that a box
containing 15 oranges out of which 12 are good and 3 are bad ones will be
approved for sale.
Question 4. A fair coin and an unbiased die are tossed. Let A be the event ‘head
appears on the coin’ and B be the event ‘3 on the die’. Check whether A and B
are independent events or not.
Question 5. A die marked 1, 2, 3 in red and 4, 5, 6 in green is tossed. Let A be
the event, ‘the number is even,’ and B be the event, ‘the number is red’. Are A
and B independent?

Question 12. A die is tossed thrice. Find the probability of getting an
odd number at least once.
Question 13. Two balls are drawn at random with replacement from a box
containing 10 black and 8 red balls. Find the probability that
(i) both balls are red.
(ii) first ball is black and second is red.
(iii) one of them is black and other is red.
Question 14. Probability of solving specific problem independently by A and B
are 1 2 and 1 3 respectively. If both try to solve the problem independently,
find the probability that (i) the problem is solved (ii) exactly one of them
solves the problem.
Question 15. One card is drawn at random from a well shuffled deck of 52
cards. In which of the following cases are the events E and F independent ?
(i) E : ‘the card drawn is a spade’ F : ‘the card drawn is an ace’
(ii) E : ‘the card drawn is black’ F : ‘the card drawn is a king’
(iii) E : ‘the card drawn is a king or queen’ F : ‘the card drawn is a queen or
jack’.
Question 16. In a hostel, 60% of the students read Hindi news paper, 40% read
English news paper and 20% read both Hindi and English news papers. A student is
selected at random.
(a) Find the probability that she reads neither Hindi nor English news
papers.
(b) If she reads Hindi news paper, find the probability that she reads English
news paper.
(c) If she reads English news paper, find the probability that she reads Hindi
news paper. Choose the correct answer in Exercises 17 and 18.
Question 17. The probability of obtaining an even prime number on each die,
when a pair of dice is rolled is
(A) 0
(B) 1 3
(C) 1 12
(D) 1 36
Question 18. Two events A and B will be independent, if
(A) A and B are mutually exclusive
(B) P(A′B′) = [1 – P(A)] [1 – P(B)]
(C) P(A) = P(B)
(D) P(A) + P(B) = 1
Question 16. In a hostel, 60% of the students read Hindi news paper, 40% read
English news paper and 20% read both Hindi and English news papers. A student is
selected at random.
(a) Find the probability that she reads neither Hindi nor English news
papers.
(b) If she reads Hindi news paper, find the probability that she reads English
news paper.
(c) If she reads English news paper, find the probability that she reads Hindi
news paper. Choose the correct answer in Exercises 17 and 18.
Question 17. The probability of obtaining an even prime number on each die,
when a pair of dice is rolled is
(A) 0
(B) 1 3
(C) 1 12
(D) 1 36
Question 18. Two events A and B will be independent, if
(A) A and B are mutually exclusive
(B) P(A′B′) = [1 – P(A)] [1 – P (B)]
(C) P(A) = P(B)
(D) P(A) + P(B) = 1
EXERCISE 13.3
Question 1. An urn contains 5 red and 5 black balls. A ball is drawn at
random, its colour is noted and is returned to the urn. Moreover, 2 additional
balls of the colour drawn are put in the urn and then a ball is drawn at random.
What is the probability that the second ball is red?
Question 2. A bag contains 4 red and 4 black balls, another bag contains 2 red
and 6 black balls. One of the two bags is selected at random and a ball is drawn
from the bag which is found to be red. Find the probability that the ball is
drawn from the first bag.
Question 3. Of the students in a college, it is known that 60% reside in hostel
and 40% are day scholars (not residing in hostel). Previous year results report
that 30% of all students who reside in hostel attain A grade and 20% of day
scholars attain A grade in their annual examination. At the end of the year, one
student is chosen at random from the college and he has an A grade, what is the
probability that the student is a hostlier?
Question 4. In answering a question on a multiple choice test, a student either
knows the answer or guesses. Let 3 4 be the probability that he knows the answer
and 1 4 be the probability that he guesses. Assuming that a student who guesses
at the answer will be correct with probability 1 4 . What is the probability
that the student knows the answer given that he answered it correctly?
Question 5. A laboratory blood test is 99% effective in detecting a certain
disease when it is in fact, present. However, the test also yields a false
positive result for 0.5% of the healthy person tested (i.e. if a healthy person
is tested, then, with probability 0.005, the test will imply he has the
disease). If 0.1 percent of the population actually has the disease, what is the
probability that a person has the disease given that his test result is positive
?
Question 6. There are three coins. One is a two headed coin (having head on both
faces), another is a biased coin that comes up heads 75% of the time and third
is an unbiased coin. One of the three coins is chosen at random and tossed, it
shows heads, what is the probability that it was the two headed coin ?
Question 7. An insurance company insured 2000 scooter drivers, 4000 car drivers
and 6000 truck drivers. The probability of an accidents are 0.01, 0.03 and 0.15
respectively. One of the insured persons meets with an accident. What is the
probability that he is a scooter driver?
Question 8. A factory has two machines A and B. Past record shows that machine A
produced 60% of the items of output and machine B produced 40% of the items.
Further, 2% of the items produced by machine A and 1% produced by machine B were
defective. All the items are put into one stockpile and then one item is chosen
at random from this and is found to be defective. What is the probability that
it was produced by machine B?
Question 9. Two groups are competing for the position on the Board of directors
of a corporation. The probabilities that the first and the second groups will
win are 0.6 and 0.4 respectively. Further, if the first group wins, the
probability of introducing a new product is 0.7 and the corresponding
probability is 0.3 if the second group wins. Find the probability that the new
product introduced was by the second group.
Question 10. Suppose a girl throws a die. If she gets a 5 or 6, she tosses a
coin three times and notes the number of heads. If she gets 1, 2, 3 or 4, she
tosses a coin once and notes whether a head or tail is obtained. If she obtained
exactly one head, what is the probability that she threw 1, 2, 3 or 4 with the
die?
Question 11. A manufacturer has three machine operators A, B and C. The first
operator A produces 1% defective items, where as the other two operators B and C
produce 5% and 7% defective items respectively. A is on the job for 50% of the
time, B is on the job for 30% of the time and C is on the job for 20% of the
time. A defective item is produced, what is the probability that it was produced
by A?
Question 12. A card from a pack of 52 cards is lost. From the remaining cards of
the pack, two cards are drawn and are found to be both diamonds. Find the
probability of the lost card being a diamond.
Question 13. Probability that A speaks truth is 4 5 . A coin is tossed. A
reports that a head appears. The probability that actually there was head is
(A) 4 5
(B) 1 2
(C) 1 5
(D) 2 5
Question 14. If A and B are two events such that A ⊂ B and P(B) ≠ 0, then
which of the following is correct?
(A) P(A| B) P(B) P(A) =
(B) P(A|B) < P(A)
(C) P(A|B) ≥ P(A)
(D) None of these
EXERCISE 13.4
Question 1. State which of the following are not the probability
distributions of a random variable. Give reasons for your answer.
Question 2. An urn contains 5 red and 2 black balls. Two balls are randomly
drawn. Let X represent the number of black balls. What are the possible values
of X? Is X a random variable ?
Question 3. Let X represent the difference between the number of heads and the
number of tails obtained when a coin is tossed 6 times. What are possible values
of X?
Question 4. Find the probability distribution of (i) number of heads in two
tosses of a coin. (ii) number of tails in the simultaneous tosses of three
coins. (iii) number of heads in four tosses of a coin.
Question 5. Find the probability distribution of the number of successes in two
tosses of a die, where a success is defined as (i) number greater than 4 (ii)
six appears on at least one die.
Question 6. From a lot of 30 bulbs which include 6 defectives, a sample of 4
bulbs is drawn at random with replacement. Find the probability distribution of
the number of defective bulbs.
Question 7. A coin is biased so that the head is 3 times as likely to occur as
tail. If the coin is tossed twice, find the probability distribution of number
of tails.
Question 8. A random variable X has the following probability distribution :
Question 9.Determine
(i) k
(ii) P(X < 3)
(iii) P(X > 6)
(iv) P(0 < X < 3)
EXERCISE 13.5
Question 1. A die is thrown 6 times. If ‘getting an odd number’ is a success,
what is the probability of (i) 5 successes? (ii) at least 5 successes? (iii) at
most 5 successes?
Question 2. A pair of dice is thrown 4 times. If getting a doublet is considered
a success, find the probability of two successes.
Question 3. There are 5% defective items in a large bulk of items. What is the
probability that a sample of 10 items will include not more than one defective
item?
Question 4. Five cards are drawn successively with replacement from a
well-shuffled deck of 52 cards. What is the probability that (i) all the five
cards are spades? (ii) only 3 cards are spades? (iii) none is a spade?
Question 5. The probability that a bulb produced by a factory will fuse after
150 days of use is 0.05. Find the probability that out of 5 such bulbs (i) none
(ii) not more than one (iii) more than one (iv) at least one will fuse after 150
days of use.
Question 6. A bag consists of 10 balls each marked with one of the digits 0 to
9. If four balls are drawn successively with replacement from the bag, what is
the probability that none is marked with the digit 0?
Question 7. In an examination, 20 questions of true-false type are asked.
Suppose a student tosses a fair coin to determine his answer to each question.
If the coin falls heads, he answers 'true'; if it falls tails, he answers
'false'. Find the probability that he answers at least 12 questions correctly.
Question 8. Suppose X has a binomial distribution B 6, 1 2 . Show that X = 3 is
the most likely outcome. (Hint : P(X = 3) is the maximum among all P(xi), xi =
0,1,2,3,4,5,6)
Question 9. On a multiple choice examination with three possible answers for
each of the five questions, what is the probability that a candidate would get
four or more correct answers just by guessing ?
Question 10. A person buys a lottery ticket in 50 lotteries, in each of which
his chance of winning a prize is 1 100 . What is the probability that he will
win a prize
(a) at least once
(b) exactly once
(c) at least twice?
Question 11. Find the probability of getting 5 exactly twice in 7 throws of a
die.
Question 12. Find the probability of throwing at most 2 sixes in 6 throws of a
single die.
Question 13. It is known that 10% of certain articles manufactured are
defective. What is the probability that in a random sample of 12 such articles,
9 are defective? In each of the following, choose the correct answer:
Question 14. In a box containing 100 bulbs, 10 are defective. The probability
that out of a sample of 5 bulbs, none is defective is
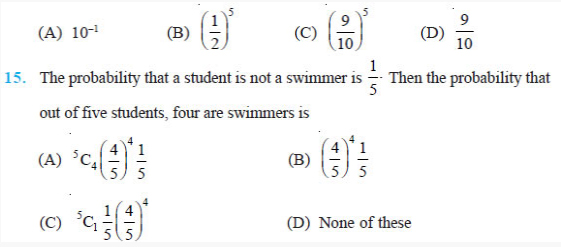
Miscellaneous Exercise
Question 1. A and B are two events such that P (A) ≠ 0. Find P(B|A), if (i) A
is a subset of B (ii) A ∩ B = φ
Question 2. A couple has two children, (i) Find the probability that both
children are males, if it is known that at least one of the children is male.
(ii) Find the probability that both children are females, if it is known that
the elder child is a female.
Question 3. Suppose that 5% of men and 0.25% of women have grey hair. A grey
haired person is selected at random. What is the probability of this person
being male? Assume that there are equal number of males and females.
Question 4. Suppose that 90% of people are right-handed. What is the probability
that at most 6 of a random sample of 10 people are right-handed?
Question 5. An urn contains 25 balls of which 10 balls bear a mark 'X' and
the remaining 15 bear a mark 'Y'. A ball is drawn at random from the urn, its
mark is noted down and it is replaced. If 6 balls are drawn in this way, find
the probability that
(i) all will bear 'X' mark.
(ii) not more than 2 will bear 'Y' mark.
(iii) at least one ball will bear 'Y' mark.
(iv) the number of balls with 'X' mark and 'Y' mark will be equal.
Question 6. In a hurdle race, a player has to cross 10 hurdles. The probability
that he will clear each hurdle is 5 6 . What is the probability that he will
knock down fewer than 2 hurdles?
Question 7. A die is thrown again and again until three sixes are obtained. Find
the probability of obtaining the third six in the sixth throw of the die.
Question 8. If a leap year is selected at random, what is the chance that it
will contain 53 tuesdays?
Question 9. An experiment succeeds twice as often as it fails. Find the
probability that in the next six trials, there will be atleast 4 successes.
Question 10. How many times must a man toss a fair coin so that the probability
of having at least one head is more than 90%?
Question 11. In a game, a man wins a rupee for a six and loses a rupee for any
other number when a fair die is thrown. The man decided to throw a die thrice
but to quit as and when he gets a six. Find the expected value of the amount he
wins / loses.
Question 12. Suppose we have four boxes A,B,C and D containing coloured marbles
as given below: One of the boxes has been selected at random and a single marble
is drawn from it. If the marble is red, what is the probability that it was
drawn from box A?, box B?, box C?
Question 13. Assume that the chances of a patient having a heart attack is 40%.
It is also assumed that a meditation and yoga course reduce the risk of heart
attack by 30% and prescription of certain drug reduces its chances by 25%. At a
time a patient can choose any one of the two options with equal probabilities.
It is given that after going through one of the two options the patient selected
at random suffers a heart attack. Find the probability that the patient followed
a course of meditation and yoga?
Question 14. If each element of a second order determinant is either zero or
one, what is the probability that the value of the determinant is positive?
(Assume that the individual entries of the determinant are chosen independently,
each value being assumed with probability 1 2 ).
Question 15. An electronic assembly consists of two subsystems, say, A and B.
From previous testing procedures, the following probabilities are assumed to be
known: P(A fails) = 0.2 P(B fails alone) = 0.15 P(A and B fail) = 0.15 Evaluate
the following probabilities (i) P(A fails|B has failed) (ii) P(A fails alone)
Question 16. Bag I contains 3 red and 4 black balls and Bag II contains 4 red
and 5 black balls. One ball is transferred from Bag I to Bag II and then a ball
is drawn from Bag II. The ball so drawn is found to be red in colour. Find the
probability that the transferred ball is black. Choose the correct answer in
each of the following:
Question 17. If A and B are two events such that P(A) ≠ 0 and P(B | A) = 1,
then
(A) A ⊂ B
(B) B ⊂ A
(C) B = φ
(D) A = φ
Question 18. If P(A|B) > P(A), then which of the following is correct :
(A) P(B|A) < P
(B) (B) P(A ∩ B) < P(A) . P(B)
(C) P(B|A) > P(B)
(D) P(B|A) = P(B)
Question 19. If A and B are any two events such that P(A) + P(B) – P(A and B)
= P(A), then
(A) P(B|A) = 1
(B) P(A|B) = 1
(C) P(B|A) = 0
(D) P(A|B) = 0