(Papers) : IIT Madras HSEE Papers-2021 (Analytical & Quantitative Ability)
Disclaimer: This website is NOT associated with CBSE, for official website of CBSE visit - www.cbse.gov.in

(Papers) : IIT Madras HSEE Papers-2021
(Analytical & Quantitative Ability)
Next two questions should be answered based on the following statements:
If the professor is well today, there is a class today.
If the professor is not well today, Jay can go to the gym.
If there is a class today, Jay cannot watch a movie.
If Jay cannot watch a movie, the world will be a happy place.
Jay cannot go to the gym.
37. Which one of the following is a valid conclusion based on the statements above?
1. Jay cannot watch a movie.
2. The world will not be a happy place.
3. The professor is not well today.
4. There is no class today.
38. Suppose in the set of statements above,
“Jay cannot go to the gym”
is replaced with
“The professor is well today”,
which of the following is NOT a valid conclusion?
1. There is a class today.
2. Jay cannot watch a movie.
3. The world will be a happy place.
4. Jay can go to the gym today.
Next three questions are based on the data given below:
The following table lists the stock prices of companies V, W, X and Y for the last five years.
39. Find the number of companies whose share prices achieved an average compounded growth rate of at least 20%
1. 1
2. 2
3. 3
4. 4
40. Which of the companies has the highest compounded average growth rate?
1. V
2. W
3. X
4. Y
41. Which of the stocks had the highest growth from year 2016 to 2017?
1. W
2. V
3. X
4. Y
42. The sum of all distinct prime factors of 100 (excluding multiplicities) is
1. 7
2. 8
3. 29
4. 28
43. Consider the following statements:
I. There are infinitely many natural numbers n such thatfor all a∈{1,…,n-1}there is aninteger b with the property a.b = 1 mod n.
II. For any natural number n ≥ 2 and any a ∈{0,…,n-1} there is an integer c such that a+c = 0 (mod n).
Which of the above statements is/are TRUE?
1. I only
2. II only
3. Neither I nor II
4. Both I and II
44. Which of the following is NOT a factor of x4-2x2+1?
1. x-1
2. x+1
3. x2-1
4. x2+1
45. Suppose x and y are two natural numbers. Let a = LCM(x,y) and b = HCF(x, y). Consider the following statements:
I. Given a and b, the values of x and y can be determined uniquely.
II.Given a and b, all common prime factors between x and y can be determined uniquely.
Which of the above statements is TRUE?
1. I only
2. II only
3. Both I and II
4. Neither I nor II
46. Area of a circle is increased by 44% when the radius is increased by x%. The value of x is
1. 10
2. 20
3. 30
4. 44
47. Suppose there are six people in a room such that any pair is either friends of each other or enemies of each other. Consider the following statements:
I. There are at least three people who are mutual enemies.
II.There are at least three people who are mutual friends.
Which of the statements is/are always TRUE?
1. Both I and II
2. At least one of I and II
3. I only
4. II only
48. Which of the options is always a composite number for any prime number p?
1. p2+1
2. 2p+3
3. 2
p+1
4. p2p-2p
49. Solve the system of linear equations
7x + 6y = 66
3x + 2y = 26
Choose a solution from the following options.
1. x = 4 and y = 6
2. x = 6 and y = 4
3. x = 4 and y = 7
4. x = 8 and y = 1
50. The product of LCM and HCF of the numbers 20, 30 and 40 is
1. 800
2. 120
3. 1200
4. 600
51. Let n ≥ 200 be a natural number. A number a is drawn uniformly at random from {1, …, n}.What is the probability that a ≥ 100 and a < 150?
1. 100/n
2. 150/n
3. 1/n
4. 50/n
52. If a word is formed by permuting five letters (v, w, x, y and z), then what is the probability that the word begins with vw?
1. 4/20
2. 8/20
3. 1/20
4. 1/120
53.
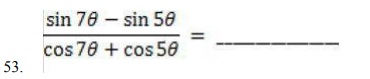
1. sin θ
2. sec θ
3. tan θ
4. cos θ
54. Persons X and Y have Rs 10,000 to share between them. Suppose X spends 10% of her money and Y spends 30% of his money. The total money left with them is 8000. What is the money left with Y?
1. Rupees 5000
2. Rupees 7000
3. Rupees 3500
4. Rupees 3000
55. A coin exchange center has coins of 1, 2, 4 and 8 denominations. The least number of coins required to exchange 150 units of currency from this center is
1. 38
2. 20
3. 18
4. 21
56. If x and y are two odd positive integers, which of the following is NOT an odd number?
1. xy
2. x2y
3. (x+y)y
4. (xy)y
57. A plane is flying at 720 kilometers per hour. Its speed in meters per second is
1. 120
2. 200
3. 180
4. 300
58. The areas of two similar triangles are 36cm2 and 64cm2 respectively. The ratio of their corresponding sides is
1. 3:4
2. 5:4
3. 2:3
4. 5:6
59. A number x is is represented as 11001 in the binary system. The decimal equivalent of x is
1. 25
2. 15
3. 19
4. 31
60. A person performs 2/7 of their journey by bike, 5/20 by bus and 13 kms on foot. The total distance
travelled is
1. 140kms
2. 75kms
3. 28kms
4. 14kms
61. The next number in the sequence 4, 8, 32, 128 is
1. 512
2. 2048
3. 1024
4. 384
62. Twelve people can finish a piece of work in 40 days. How many people are needed to finish the same work in 60 days?
1. 8
2. 10
3. 5
4. 12
63. Suppose Ram and Shyam have Rupees 1000 each. Ram deposits his money in a bank with a simple interest of 10% while Shyam does the same with a compound interest of 10%. If interests are computed annually, the difference between their withdrawal amounts after four years (rounded off to the nearest integer) would be
1. Rupees 50
2. Rupees 64
3. Rupees 150
4. Rupees 750
64. There are six people in a room. What is the total number of ways of choosing a four-member team with one of them designated as the chairman?
1. 30
2. 60
3. 15
4. (36)2
65. Using only three given letters of the alphabet, the total number of words possible with exactly five charactersis
1. 53
2. 35
3. 25
4. 55
66. Suppose the manufacturer of a chair gains 20%, wholesale dealer 10% and the retailer 20%. If the retail price of the chair is 15840, the manufacturing cost of the chair is
1. 10000
2. 1000
3. 12000
4. 9000
67. Let X, Y and Z be sets. Which one of the following is always TRUE?
1. X ∩ Y ⊆ X ∩ Y ∩ Z
2. (X ∩ Y) ∪ Z ⊆ (X ∪ Z) ∩ (Y ∪ Z)
3. (X ∪ Y) - Z ≠(X - Z) ∪ (Y - Z)
4. X = (X ∪ Y) ∪(Y - X)
68. Suppose the following diagram depicts the road network between five cities named V, W, X, Y and Z. A line between two cities indicates a direct road connection and the cost of driving along the road is given as its label.
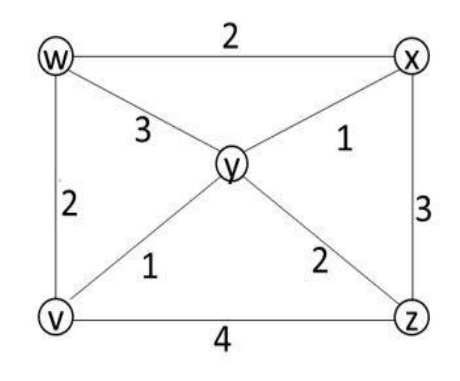
Sudhi wants to start from city W and return to W after visiting every city only once. The minimum cost Sudhi incurs to achieve his goal is
1. 8
2. 10
3. 11
4. 13
69. The fees (in lakhs of rupees) collected by a school in the last five years is 2, 4, 3, 5 and 6. What is the variance?
1. 18
2. 4
3. 16
4. 2
70. A student has an average of 40 marks in four exams. How much should she score in the fifth exam so that her average across five exams is 45?
1. 45
2. 60
3. 65
4. 90
71. The LCM of (x+1), (x-1) and (2x2+x-1) is
1. x3-1
2. 2x3 - x2 -2x+1
3. 2x3 + x2 -2x+1
4. 2x3 - x2 + 2x - 1
72. The length of the minute hand of a clock is 20cm. The distance traveled by the outer end of the hand in 24 minutes is
1. 16π
2. 20π
3. 8π
4. 4π/3
Download Free e-Books for CBSE Students
Courtesy: HSEE
