
NCERT Mathematics Question Paper (Class - 12)
:: Chapter 1 - Number System ::
Q1. Determine whether each of the following relations are
reflexive, symmetric and transitive:
(ii) Relation R in the set N of natural numbers defined as
R = {(x, y) : y = x + 5 and x < 4}
(iii) Relation R in the set A = {1, 2, 3, 4, 5, 6} as
R = {(x, y) : y is divisible by x}
(iv) Relation R in the set Z of all integers defined as
R = {(x, y) : x – y is an integer}
Q 1. Determine whether each of the following relations are reflexive,
symmetric and transitive:
(i) Relation R in the set A = {1, 2, 3, ..., 13, 14} defined
as
R = {(x, y) : 3x – y = 0}
Q 1.Determine whether each of the following relations are reflexive,
symmetric and transitive:
(v) Relation R in the set A of human beings in a town at a
particular time given by
(a) R = {(x, y) : x and y work at the same place}
(b) R = {(x, y) : x and y live in the same locality}
(c) R = {(x, y) : x is exactly 7 cm taller than y}
(d) R = {(x, y) : x is wife of y}
(e) R = {(x, y) : x is father of y}
2. Show that the relation R in the set R of real numbers, defined as
R = {(a, b) : a ? b2} is neither reflexive nor symmetric nor transitive.
3. Check whether the relation R defined in the set {1, 2, 3, 4, 5, 6} as
R = {(a, b) : b = a + 1} is reflexive, symmetric or transitive.
4. Show that the relation R in R defined as R = {(a, b) : a ? b}, is reflexive
and transitive but not symmetric.
5. Check whether the relation R in R defined by R = {(a, b) : a ? b3} is
reflexive, symmetric or transitive.
6. Show that the relation R in the set {1, 2, 3} given by R = {(1, 2), (2, 1)}
is symmetric but neither reflexive nor transitive.
7. Show that the relation R in the set A of all the books in a library of a
college, given by R = {(x, y) : x and y have same number of pages} is an
equivalence relation.
8. Show that the relation R in the set A = {1, 2, 3, 4, 5} given by
R = {(a, b) : |a – b| is even}, is an equivalence relation. Show that all
the elements of {1, 3, 5} are related to each other and all the elements of {2,
4} are related to each other. But no element of {1, 3, 5} is related to any
element of {2, 4}.
9. Show that each of the relation R in the set A = {x ? Z : 0 ? x ? 12},
given by
(i) R = {(a, b) : |a – b| is a multiple of 4}
(ii) R = {(a, b) : a = b}
:: Chapter 2 - Inverse Trigonometric Functions ::
EXERCISE
Question 1. Find the principal values of the following:

Question 6. Show that the relation R in the set {1, 2, 3}
given by R = {(1, 2), (2, 1)} is symmetric but neither reflexive nor transitive.
Question 7. Show that the relation R in the set A of all the
books in a library of a college, given by R = {(x, y) : x and y have same number
of pages} is an equivalence relation.
Question 8. Show that the relation R in the set A = {1, 2,
3, 4, 5} given by R = {(a, b) :
|a – b| is even}, is an equivalence relation. Show that all the elements of
{1, 3, 5} are related to each other and all the elements of {2, 4} are related
to each other. But no element of {1, 3, 5} is related to any element of {2, 4}.
Question 9. Show that each of the relation R in the set A = {x ∈ Z : 0 ≤ x ≤
12}, given by (i) R = {(a, b) : |a – b| is a multiple of 4} (ii) R = {(a, b) : a
= b} is an equivalence relation. Find the set of all elements related to 1 in
each case.
Question 10. Give an example of a relation. Which is
(i) Symmetric but neither reflexive nor transitive.
(ii) Transitive but neither reflexive nor symmetric.
(iii) Reflexive and symmetric but not transitive.
(iv) Reflexive and transitive but not symmetric.
(v) Symmetric and transitive but not reflexive.
Question 11. Show that the relation R in the set A of points
in a plane given by R = {(P, Q) : distance of the point P from the origin is
same as the distance of the point Q from the origin}, is an equivalence
relation. Further, show that the set of all points related to a point P ≠ (0, 0)
is the circle passing through P with origin as centre.
Question 12. Show that the relation R defined in the set A of
all triangles as R = {(T1, T2) : T1 is similar to T2}, is equivalence relation.
Consider three right angle triangles T1 with sides 3, 4, 5, T2 with sides 5, 12,
13 and T3 with sides 6, 8, 10. Which triangles among T1, T2 and T3 are related?
Question 13. Show that the relation R defined in the set A of
all polygons as R = {(P1, P2) : P1 and P2 have same number of sides}, is an
equivalence relation. What is the set of all elements in A related to the right
angle triangle T with sides 3, 4 and 5?
Question 14. Let L be the set of all lines in XY plane and R
be the relation in L defined as R = {(L1, L2) : L1 is parallel to L2}. Show that
R is an equivalence relation. Find the set of all lines related to the line y =
2x + 4.
Question 15. Let R be the relation in the set {1, 2, 3, 4}
given by R = {(1, 2), (2, 2), (1, 1), (4,4), (1, 3), (3, 3), (3, 2)}. Choose the
correct answer.
(A) R is reflexive and symmetric but not transitive.
(B) R is reflexive and transitive but not symmetric.
(C) R is symmetric and transitive but not reflexive.
(D) R is an equivalence relation.
Question 16. Let R be the relation in the set N given by R
= {(a, b) : a = b – 2, b > 6}. Choose the correct answer.
(A) (2, 4) ∈ R
(B) (3, 8) ∈ R
(C) (6, 8) ∈ R
(D) (8, 7) ∈ R
EXERCISE
Question 1. Show that the function f : R → R defined by f (x)
= 1 x is one-one and onto, where R is the set of all non-zero real numbers. Is
the result true, if the domain R is replaced by N with co-domain being same as
R?
Question 2. Check the injectivity and surjectivity of the
following functions:
(i) f : N → N given by f (x) = x2
(ii) f : Z → Z given by f (x) = x2
(iii) f : R → R given by f (x) = x2
(iv) f : N → N given by f (x) = x3
(v) f : Z → Z given by f (x) = x3
Question 3. Prove that the Greatest Integer Function f :
R→R, given by f (x) = [x], is neither one-one nor onto, where [x] denotes
the greatest integer less than or equal to x.
Question 4. Show that the Modulus Function f : R→R, given
by f (x) = | x |, is neither oneone nor onto, where | x | is x, if x is positive
or 0 and | x | is – x, if x is negative. 5. Show that the Signum Function f :
R→R, given by
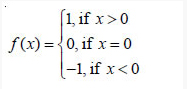
is neither one-one nor onto.
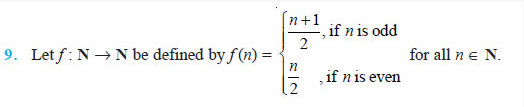
State whether the function f is bijective. Justify your
answer.
Question 10. Let A = R – {3} and B = R – {1}. Consider the
function f : A → B defined by

Question 11. Let f : R → R be defined as f(x) = x4. Choose
the correct answer.
(A) f is one-one onto (B) f is many-one onto
(C) f is one-one but not onto
(D) f is neither one-one nor onto.
Question 12. Let f : R → R be defined as f (x) = 3x.
Choose the correct answer.
(A) f is one-one onto
(B) f is many-one onto
(C) f is one-one but not onto
(D) f is neither one-one nor onto.
EXERCISE

 EXERCISE
EXERCISE



Show that is commutative and associative. Find the identity
element for on A, if any.
Question 12. State whether the following statements are true
or false. Justify.
(i) For an arbitrary binary operation on a set N, a a = a ∀ a
∈ N.
(ii) If is a commutative binary operation on N, then a (b c) = (c b) a
Question 13. Consider a binary operation on N defined as a b
= a3 + b3. Choose the correct answer.
(A) Is both associative and commutative?
(B) Is commutative but not associative?
(C) Is associative but not commutative?
(D) Is neither commutative nor associative?

Define the relation R in P(X) as follows: For subsets A, B in
P(X), ARB if and only if A ⊂ B. Is R an equivalence relation on P(X)? Justify
your answer.
Question 9. Given a non-empty set X, consider the binary
operation :
P(X) × P(X) → P(X) given by A B = A ∩ B ∀ A, B in P(X), where
P(X) is the power set of X. Show that X is the identity element for this
operation and X is the only invertible element in P(X) with respect to the
operation
Question 10. Find the number of all onto functions from the
set {1, 2, 3, ... , n} to itself.
Question 11. Let S = {a, b, c} and T = {1, 2, 3}. Find F–1
of the following functions F from S to T, if it exists.
(i) F = {(a, 3), (b, 2), (c, 1)}
(ii) F = {(a, 2), (b, 1), (c, 1)}
Question 12. Consider the binary operations : R × R → R and o
: R × R → R defined as a b = |a – b| and a o b = a, ∀ a, b ∈ R. Show that is
commutative but not associative, o is associative but not commutative. Further,
show that ∀ a, b, c ∈ R, a (b o c) = (a b) o (a b). [If it is so, we say that
the operation distributes over the operation o]. Does o distribute over ?
Justify your answer.
Question 13. Given a non-empty set X, let : P(X) × P(X) → P(X)
be defined as A * B = (A – B) ∪ (B – A), ∀ A, B ∈ P(X). Show that the empty set
φ is the identity for the operation and all the elements A of P(X) are
invertible with A–1 = A. (Hint : (A – φ) ∪ (φ – A) = A and (A – A) ∪ (A – A) = A
A = φ).
Question 14. Define a binary operation on the set {0, 1, 2,
3, 4, 5} as



:: Chapter 3 - Matrix ::
EXERCISE
Question 1. In the matrix
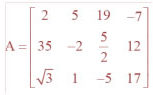 , write
, write
(i) The order of the matrix, (ii) The number of elements,
(iii) Write the elements a13, a21, a33, a24, a23.
Question 2. If a matrix has 24 elements, what are the
possible orders it can have? What, if it has 13 elements?
Question 3. If a matrix has 18 elements, what are the
possible orders it can have? What, if it has 5 elements ?
Question 4. Construct a 2 × 2 matrix, A = [aij], whose
elements are given by:
(i)aij=(i + j)2/2
Question 4. Construct a 2 × 2 matrix, A = [aij], whose
elements are given by:
(ii)aij=i/j
Question 4. Construct a 2 × 2 matrix, A = [aij], whose
elements are given by:
(iii)aij=(i + 2j)2/2
Question 5. Construct a 3 × 4 matrix, whose elements are
given by:
(i)aij=1/2| -3i + j |
Question 5. Construct a 3 × 4 matrix, whose elements are
given by:
(ii)aij=2i - j
Question 6. Find the values of x, y and z from the
following equations:
(i)
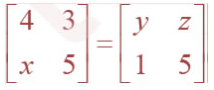
Question 6. Find the values of x, y and z from the
following equations:
(ii)
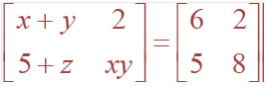
Question 6. Find the values of x, y and z from the
following equations:
(iii)
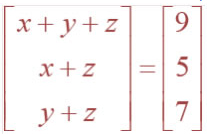
Question 7. Find the value of a, b, c and d from the
equation
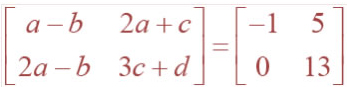
Question 8
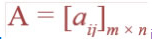 .is a
square matrix, if
.is a
square matrix, if
(A) m < n (B) m > n (C) m = n (D) None of these
Question 9.Which of the given values of x and y make the
following pair of matrices equal
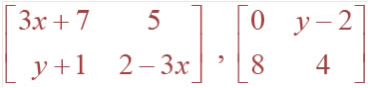
Question 10. The number of all possible matrices of order
3 × 3 with each entry 0 or 1 is:
EXERCISE
=Question 1. Let
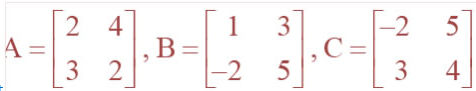 Find
each of the following:
Find
each of the following:
(i) A + B (ii) A – B (iii) 3A – C
=Question 1. Let
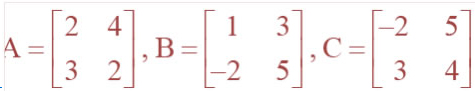 Find
each of the following:
Find
each of the following:
(iv) AB (v) BA
=Question 2. Compute the following:
=Question 3. Compute the indicated products.
=Question 4.
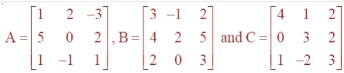 If ,
then compute (A+B) and (B – C). Also, verify that A + (B – C) = (A + B) – C.
If ,
then compute (A+B) and (B – C). Also, verify that A + (B – C) = (A + B) – C.
=Question 5.
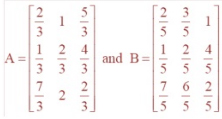 If ,
then compute 3A – 5B.
If ,
then compute 3A – 5B.
=Question 6. Simplify
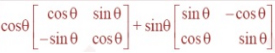
:: Chapter 4 - Determinants ::
Exercise
Question 1. Evaluate the determinants in Exercises 1 and 2.
Question 2. Evaluate the determinants in Exercises 1 and 2.
Question 3. If
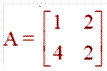 ,
then show that | 2A | = 4 | A |
,
then show that | 2A | = 4 | A |
Question 4. If
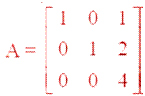 ,
then show that | 3 A | = 27 | A |
,
then show that | 3 A | = 27 | A |
Question 5. Evaluate the determinants
Question 6. If
 ,
find | A |
,
find | A |
Question 7. Find values of x, if

Question 8. If
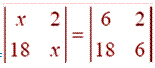 ,
then x is equal to
,
then x is equal to
Exercise
Using the property of determinants and without expanding in
Exercises 1 to 7, prove That
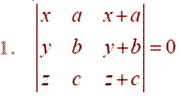
Using the property of determinants and without expanding in Exercises 1 to 7,
prove That
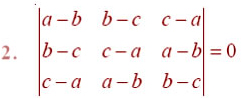
Using the property of determinants and without expanding in Exercises 1 to 7,
prove That
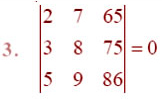
Using the property of determinants and without expanding in Exercises 1 to 7,
prove That
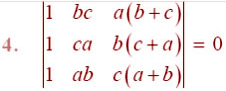
Using the property of determinants and without expanding in Exercises 1 to 7,
prove That
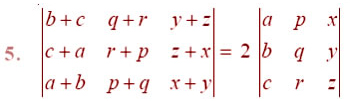
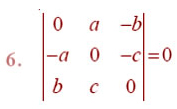
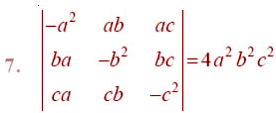
By using properties of determinants, in Exercises 8 to 14, show that:
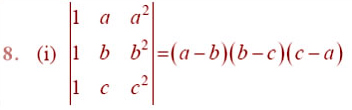
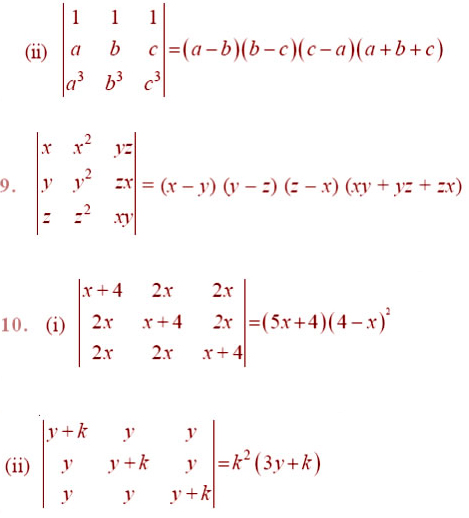
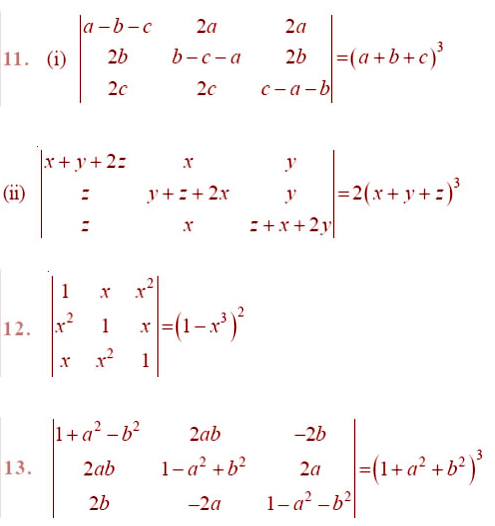
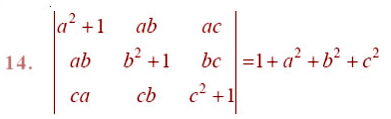
Question 15.Let A be a square matrix of order 3 × 3, then | kA| is equal to
(A) k| A|
(B) k2 | A|
(C) k3 | A|
(D) 3k | A |
Question 16. Which of the following is correct?
(A) Determinant is a square matrix.
(B) Determinant is a number associated to a matrix.
(C) Determinant is a number associated to a square matrix.
(D) None of these
Exercise
Question 1. Find area of the triangle with vertices at the
point given in each of the following :
(i) (1, 0), (6, 0), (4, 3)
(ii) (2, 7), (1, 1), (10, 8)
(iii) (–2, –3), (3, 2), (–1, –8)
Question 2. Show that points A (a, b + c), B (b, c + a), C
(c, a + b) are collinear.
Question 3. Find values of k if area of triangle is 4 sq.
units and vertices are
(i) (k, 0), (4, 0), (0, 2)
(ii) (–2, 0), (0, 4), (0, k)
Question 4.
(i) Find equation of line joining (1, 2) and (3, 6) using determinants.
(ii) Find equation of line joining (3, 1) and (9, 3) using determinants.
Question 5. If area of triangle is 35 sq units with vertices
(2, – 6), (5, 4) and (k, 4). Then k is
(A) 12 (B) –2 (C) –12, –2 (D) 12, –2
Exercise
Write Minors and Cofactors of the elements of following
determinants:

Exercise
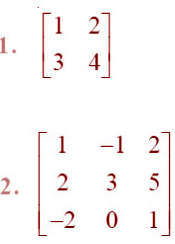
=Find adjoint of each of the matrices in Exercises 1 and 2.
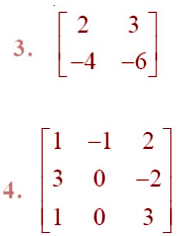
=Verify A (adj A) = (adj A) A = |A| I in Exercises 3 and 4
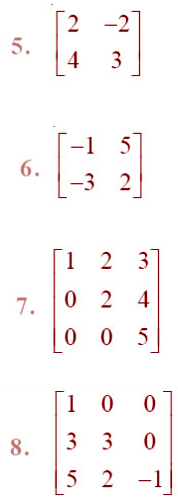
=Find the inverse of each of the matrices (if it exists) given
in Exercises 5 to 11.


17. Let A be a nonsingular square matrix of order 3 × 3. Then
|adj A| is equal to
(A) |A|
(B) |A|2
(C) |A|3
(D) 3|A|
18. If A is an invertible matrix of order 2, then det (A–1) is
equal to
(A) det
(A) (B)1/det (A)
(C) 1
(D) 0
Exercise
Question 1. x + 2y = 2 and 2x + 3y = 3
Question 2. 2x – y = 5 and x + y = 4
Question 3. x + 3y = 5 and 2x + 6y = 8
Question 4. x + y + z = 1 , 2x + 3y + 2z = 2 and ax + ay + 2az =
4
Question 3x–y – 2z = 2, 2y – z =-1 and –3x – 5y = 3
Question 6. 5x – y + 4z = 5,2x + 3y + 5z = 2 and 5x – 2y + 6z =
–1
Solve system of linear equations, using matrix method, in
Exercises 7 to 14.
Question 7. 5x + 2y = 4 and 7x + 3y = 5
Question 8. 2x – y = –2 and 3x + 4y = 3
Question 9. 4x – 3y = 3 and 3x – 5y = 7
Question 10. 5x + 2y = 3 and 3x + 2y = 5
Question 11. 2x + y + z = 1, x – 2y – z =3/2 and 3y – 5z = 9
Question 12. x – y + z = 4, 2x + y – 3z = 0 and x + y + z = 2
Question 13. 2x + 3y +3 z = 5, x – 2y + z = – 4 and 3x – y – 2z
= 3
Question 14. x – y + 2z = 7,3x + 4y – 5z = – 5 and 2x – y + 3z =
12
Question 15. If
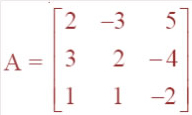 , find A–1. Using A–1 solve the system of equations 2x – 3y + 5z = 11 3x + 2y –
4z = – 5 x + y – 2z = – 3
, find A–1. Using A–1 solve the system of equations 2x – 3y + 5z = 11 3x + 2y –
4z = – 5 x + y – 2z = – 3
Question 16. The cost of 4 kg onion, 3 kg wheat and 2 kg rice is
Rs 60. The cost of 2 kg onion, 4 kg wheat and 6 kg rice is Rs 90. The cost of 6
kg onion 2 kg wheat and 3 kg rice is Rs 70. Find cost of each item per kg by
matrix method.
:: Chapter 6 - Application of Derivatives ::
EXERCISE
Question 1. Find the rate of change of the area of a circle with respect to
its radius r when (a) r = 3 cm (b) r = 4 cm
Question 2. The volume of a cube is increasing at the rate of 8 cm3/s. How
fast is the surface area increasing when the length of an edge is 12 cm?
Question 3. The radius of a circle is increasing uniformly at the rate of 3
cm/s. Find the rate at which the area of the circle is increasing when the
radius is 10 cm.
Question 4. An edge of a variable cube is increasing at the rate of 3 cm/s.
How fast is the volume of the cube increasing when the edge is 10 cm long?
Question 5. A stone is dropped into a quiet lake and waves move in circles at
the speed of 5 cm/s. At the instant when the radius of the circular wave is 8
cm, how fast is the enclosed area increasing? 6. The radius of a circle is
increasing at the rate of 0.7 cm/s. What is the rate of increase of its
circumference?
Question 7. The length x of a rectangle is decreasing at the rate of 5
cm/minute and the width y is increasing at the rate of 4 cm/minute. When x = 8cm
and y = 6cm, find the rates of change of (a) the perimeter, and (b) the area of
the rectangle.
Question 8. A balloon, which always remains spherical on inflation, is being
inflated by pumping in 900 cubic centimetres of gas per second. Find the rate at
which the radius of the balloon increases when the radius is 15 cm.
Question 9. A balloon, which always remains spherical has a variable radius.
Find the rate at which its volume is increasing with the radius when the later
is 10 cm. 10. A ladder 5 m long is leaning against a wall. The bottom of the
ladder is pulled along the ground, away from the wall, at the rate of 2cm/s. How
fast is its height on the wall decreasing when the foot of the ladder is 4 m
away from the wall
Question 11. A particle moves along the curve 6y = x3 +2. Find the points on
the curve at which the y-coordinate is changing 8 times as fast as the
x-coordinate.
Question 12. The radius of an air bubble is increasing at the rate of 1 2
cm/s. At what rate is the volume of the bubble increasing when the radius is 1
cm?
Question 13. A balloon, which always remains spherical, has a variable
diameter 3 (2 1) 2 x + . Find the rate of change of its volume with respect to
x.
Question 14. Sand is pouring from a pipe at the rate of 12 cm3/s. The falling
sand forms a cone on the ground in such a way that the height of the cone is
always one-sixth of the radius of the base. How fast is the height of the sand
cone increasing when the height is 4 cm?
Question 15. The total cost C(x) in Rupees associated with the production of
x units of an item is given by C(x) = 0.007x3 – 0.003x2 + 15x + 4000. Find the
marginal cost when 17 units are produced.
Question 16. The total revenue in Rupees received from the sale of x units of
a product is given by R(x) = 13x2 + 26x + 15. Find the marginal revenue when x =
7.
Question 17. The rate of change of the area of a circle with respect to
its radius r at r = 6 cm is
(A) 10π
(B) 12π
(C) 8π
(D) 11π
Question 18. The total revenue in Rupees received from the sale of x units
of a product is given by R(x) = 3x2 + 36x + 5. The marginal revenue, when x = 15
is
(A) 116
(B) 96
(C) 90
(D) 126
EXERCISE
Question 1. Show that the function given by f (x) = 3x + 17 is strictly
increasing on R.
Question 2. Show that the function given by f (x) = e2x is strictly
increasing on R.
Question 3. Show that the function given by f (x) = sin x is (a) strictly
increasing in 0, 2 (b) strictly decreasing in , 2 (c) neither increasing nor
decreasing in (0, π)
Question 4. Find the intervals in which the function f given by f (x) = 2x2 –
3x is (a) strictly increasing (b) strictly decreasing
Question 5. Find the intervals in which the function f given by f (x) = 2x3 –
3x2 – 36x + 7 is (a) strictly increasing (b) strictly decreasing
Question 6. Find the intervals in which the following functions are
strictly increasing or decreasing:
(a) x2 + 2x – 5
(b) 10 – 6x – 2x2
(c) –2x3 – 9x2 – 12x + 1
(d) 6 – 9x – x2
(e) (x + 1)3 (x – 3)3
Question 7. Show that log(1 ) 2 2 y x x x = + −+ , x > – 1, is an increasing
function of x throughout its domain.
Question 8. Find the values of x for which y = [x(x – 2)]2 is an increasing
function.
Question 9. Prove that 4sin (2 cos ) y θ = −θ + θ is an increasing function
of θ in 0, 2
Question 10. Prove that the logarithmic function is strictly increasing on
(0, ∞).
Question 11. Prove that the function f given by f (x) = x2 – x + 1 is neither
strictly increasing nor strictly decreasing on (– 1, 1)
Question 12. Which of the following functions are strictly decreasing on
0, 2?
(A) cos x
(B) cos 2x
(C) cos 3x
(D) tan x
Question 13. On which of the following intervals is the function f given by f
(x) = x100 + sin x –1 strictly decreasing ? (A) (0,1) (B) , 2 (D) None of these
Question 14. Find the least value of a such that the function f given by f
(x) = x2 + ax + 1 is strictly increasing on (1, 2).
Question 15. Let I be any interval disjoint from (–1, 1). Prove that the
function f given by f (x) x 1 x = + is strictly increasing on I.
Question 16. Prove that the function f given by f (x) = log sin x is strictly
increasing on 0, 2and strictly decreasing on .
Question 17. Prove that the function f given by f (x) = log cos x is strictly
decreasing on 0, 2 ⎠ and strictly increasing on , 2 .
Question 18. Prove that the function given by f (x) = x3 – 3x2 + 3x – 100 is
increasing in R.
Question 19. The interval in which y = x2 e–x is increasing is
(A) (– ∞, ∞)
(B) (– 2, 0)
(C) (2, ∞)
(D) (0, 2)
EXERCISE
Question 1. Find the slope of the tangent to the curve y = 3x4 – 4x at x = 4.
Question 2. Find the slope of the tangent to the curve 1, 2 2 y x x x − = ≠ −
at x = 10.
Question 3. Find the slope of the tangent to curve y = x3 – x + 1 at the
point whose x-coordinate is 2.
Question 4. Find the slope of the tangent to the curve y = x3 –3x + 2 at the
point whose x-coordinate is 3.
Question 5. Find the slope of the normal to the curve x = acos3 θ, y = asin3
θ at . 4 π θ =
Question 6. Find the slope of the normal to the curve x = 1− asinθ, y = bcos2
θ at . 2 π θ =
Question 7. Find points at which the tangent to the curve y = x3 – 3x2 – 9x +
7 is parallel to the x-axis.
Question 8. Find a point on the curve y = (x – 2)2 at which the tangent is
parallel to the chord joining the points (2, 0) and (4, 4).
Question 9. Find the point on the curve y = x3 – 11x + 5 at which the tangent
is y = x – 11.
Question 10. Find the equation of all lines having slope – 1 that are
tangents to the curve 1 1 y x = − , x ≠ 1.
Question 11. Find the equation of all lines having slope 2 which are tangents
to the curve 1 3 y x = − , x ≠ 3.
Question 12. Find the equations of all lines having slope 0 which are tangent
to the curve 2 1 . 2 3 y x x = − +
Question 13. Find points on the curve 2 2 1 9 16 x + y = at which the
tangents are (i) parallel to x-axis (ii) parallel to y-axis.
Question 14. Find the equations of the tangent and normal to the given
curves at the indicated points:
(i) y = x4 – 6x3 + 13x2 – 10x + 5 at (0, 5)
(ii) y = x4 – 6x3 + 13x2 – 10x + 5 at (1, 3)
(iii) y = x3 at (1, 1)
(iv) y = x2 at (0, 0)
(v) x = cos t, y = sin t at 4 t π =1
Question 15. Find the equation of the tangent line to the curve y = x2 – 2x
+7 which is (a) parallel to the line 2x – y + 9 = 0 (b) perpendicular to the
line 5y – 15x = 13.
Question 16. Show that the tangents to the curve y = 7x3 + 11 at the points
where x = 2 and x = – 2 are parallel.
Question 17. Find the points on the curve y = x3 at which the slope of the
tangent is equal to the y-coordinate of the point.
Question 18. For the curve y = 4x3 – 2x5, find all the points at which the
tangent passes through the origin.
Question 19. Find the points on the curve x2 + y2 – 2x – 3 = 0 at which the
tangents are parallel to the x-axis.
Question 20. Find the equation of the normal at the point (am2,am3) for the
curve ay2 = x3.
Question 21. Find the equation of the normals to the curve y = x3 + 2x + 6
which are parallel to the line x + 14y + 4 = 0.
Question 22. Find the equations of the tangent and normal to the parabola y2
= 4ax at the point (at2, 2at).
Question 23. Prove that the curves x = y2 and xy = k cut at right angles* if
8k2 = 1.
Question 24. Find the equations of the tangent and normal to the hyperbola 2
2 2 2 1 x y a b − = at the point (x0, y0).
Question 25. Find the equation of the tangent to the curve y = 3x − 2 which
is parallel to the line 4x − 2y + 5 = 0 . Choose the correct answer in Exercises
26 and 27.
Question 26. The slope of the normal to the curve y = 2x2 + 3 sin x at x =
0 is
(A) 3
(B) 1 3
(C) –3
(D) 1 3 −
Question 27. The line y = x + 1 is a tangent to the curve y2 = 4x at the
point
(A) (1, 2)
(B) (2, 1)
(C) (1, – 2)
(D) (– 1, 2)
EXERCISE
Question 1. Using differentials, find the approximate value of each of the
following up to 3 places of decimal.
(i) 25.3
(ii) 49.5
(iii) 0.6
(iv) 1 (0.009)3
(v) 1 (0.999)10
(vi) 1 (15)4
(vii) 1 (26)3
(viii) 1 (255)4
(ix) 1 (82)4
(x) 1 (401)2
(xi) 1 (0.0037)2
(xii) 1 (26.57)3
(xiii) 1 (81.5)4
(xiv) 3 (3.968)2
(xv) 1 (32.15)5
Question 2. Find the approximate value of f (2.01), where f (x) = 4x2 + 5x +
2.
Question 3. Find the approximate value of f (5.001), where f (x) = x3 – 7x2 +
15.
Question 4. Find the approximate change in the volume V of a cube of side x
metres caused by increasing the side by 1%.
Question 5. Find the approximate change in the surface area of a cube of side
x metres caused by decreasing the side by 1%.
Question 6. If the radius of a sphere is measured as 7 m with an error of
0.02 m, then find the approximate error in calculating its volume.
Question 7. If the radius of a sphere is measured as 9 m with an error of
0.03 m, then find the approximate error in calculating its surface area.
Question 8. If f(x) = 3x2 + 15x + 5, then the approximate value of f
(3.02) is (A) 47.66 (B) 57.66 (C) 67.66 (D) 77.66 9. The approximate change in
the volume of a cube of side x metres caused by increasing the side by 3% is
(A) 0.06 x3 m3
(B) 0.6 x3 m3
(C) 0.09 x3 m3
(D) 0.9 x3 m3
EXERCISE
Question 1. Find the maximum and minimum values, if any, of the following
functions given by
(i) f
(x) = (2x – 1)2 + 3
(ii) f (x) = 9x2 + 12x + 2
(iii) f
(x) = –
(x – 1)2 + 10
(iv) g
(x) = x3 +
Question 1. It is given that at x = 1, the function x4 – 62x2 + ax + 9
attains its maximum value, on the interval [0, 2]. Find the value of a.
Question 2. Find the maximum and minimum values of x + sin 2x on [0, 2π].
Question 3. Find two numbers whose sum is 24 and whose product is as large as
possible.
Question 4. Find two positive numbers x and y such that x + y = 60 and xy3 is
maximum.
Question 5. Find two positive numbers x and y such that their sum is 35 and
the product x2 y5 is a maximum.
Question 6. Find two positive numbers whose sum is 16 and the sum of whose
cubes is minimum.
Question 7. A square piece of tin of side 18 cm is to be made into a box
without top, by cutting a square from each corner and folding up the flaps to
form the box. What should be the side of the square to be cut off so that the
volume of the box is the maximum possible.
Question 8. A rectangular sheet of tin 45 cm by 24 cm is to be made into a
box without top, by cutting off square from each corner and folding up the
flaps. What should be the side of the square to be cut off so that the volume of
the box is maximum ?
Question 9. Show that of all the rectangles inscribed in a given fixed
circle, the square has the maximum area.
Question 10. Show that the right circular cylinder of given surface and
maximum volume is such that its height is equal to the diameter of the base.
Question 11. Of all the closed cylindrical cans (right circular), of a given
volume of 100 cubic centimetres, find the dimensions of the can which has the
minimum surface area?
Question 12. A wire of length 28 m is to be cut into two pieces. One of the
pieces is to be made into a square and the other into a circle. What should be
the length of the two pieces so that the combined area of the square and the
circle is minimum?
Question 13. Prove that the volume of the largest cone that can be inscribed
in a sphere of radius R is 8 27 of the volume of the sphere.
Question 14. Show that the right circular cone of least curved surface and
given volume has an altitude equal to 2 time the radius of the base.
Question 15. Show that the semi-vertical angle of the cone of the maximum
volume and of given slant height is tan−1 2 .
Question 16. Show that semi-vertical angle of right circular cone of given
surface area and maximum volume is sin 1 1
Miscellaneous Exercise on Chapter 6
Question 1. Using differentials, find the approximate value of each of the
following: (a) 1 17 4 81 (b) ( ) 1 33 5 −
Question 2. Show that the function given by f (x) log x x = has maximum at x
= e.
Question 3. The two equal sides of an isosceles triangle with fixed base b
are decreasing at the rate of 3 cm per second. How fast is the area decreasing
when the two equal sides are equal to the base
Question 4. Find the equation of the normal to curve x2 = 4y which passes
through the point (1, 2).
Question 5. Show that the normal at any point θ to the curve x = a cosθ + a θ
sin θ, y = a sinθ – aθ cosθ is at a constant distance from the origin.
Question 6. Find the intervals in which the function f given by ( ) 4sin 2
cos 2 cos f x x x x x x − − = + is
(i) increasing
(ii) decreasing.
Question 7. Find the intervals in which the function f given by 3 3 f (x)
x 1 , x 0 x = + ≠ is
(i) increasing
(ii) decreasing.
Question 8. Find the maximum area of an isosceles triangle inscribed in the
ellipse 2 2 2 2 1 x y a b + = with its vertex at one end of the major axis.
Question 9. A tank with rectangular base and rectangular sides, open at the
top is to be constructed so that its depth is 2 m and volume is 8 m3. If
building of tank costs Rs 70 per sq metres for the base and Rs 45 per square
metre for sides. What is the cost of least expensive tank?
Question 10. The sum of the perimeter of a circle and square is k, where k is
some constant. Prove that the sum of their areas is least when the side of
square is double the radius of the circle.
Question 11. A window is in the form of a rectangle surmounted by a
semicircular opening. The total perimeter of the window is
Question 12. m. Find the dimensions of the window to admit maximum light
through the whole opening.
Question 13. A point on the hypotenuse of a triangle is at distance a and b
from the sides of the triangle. Show that the maximum length of the hypotenuse
is 2 2 3 (a3 + b3 )2 .
Question 14. Find the points at which the function f given by f (x) = (x –
2)4 (x + 1)3 has
(i) local maxima
(ii) local minima
(iii) point of inflexion
14. Find the absolute maximum and minimum values of the function f given by f
(x) = cos2 x + sin x, x ∈ [0, π]
Question 15. Show that the altitude of the right circular cone of maximum
volume that can be inscribed in a sphere of radius r is 4 3 r .
Question 16. Let f be a function defined on [a, b] such that f ′(x) > 0, for
all x ∈ (a, b). Then prove that f is an increasing function on (a, b).
Question 17. Show that the height of the cylinder of maximum volume that can
be inscribed in a sphere of radius R is 2R 3 . Also find the maximum volume.
Question 18. Show that height of the cylinder of greatest volume which can be
inscribed in a right circular cone of height h and semi vertical angle α is
one-third that of the cone and the greatest volume of cylinder is 4 3 tan2 27 πh
α . Choose the correct answer in the Exercises from 19 to 24.
Question 19. A cylindrical tank of radius 10 m is being filled with wheat
at the rate of 314 cubic metre per hour. Then the depth of the wheat is
increasing at the rate of
(A) 1 m3/h
(B) 0.1 m3/h
(C) 1.1 m3/h
(D) 0.5 m3/h
Question 20. The slope of the tangent to the curve x = t2 + 3t – 8, y =
2t2 – 2t – 5 at the point (2,– 1) is
(A) 22 7
(B) 6 7
(C) 7 6
(D) 6 7
Question 21. The line y = mx + 1 is a tangent to the curve y2 = 4x if the
value of m is
(A) 1
(B) 2
(C) 3
(D) 1 2
Question 22. The normal at the point (1,1) on the curve 2y + x2 = 3 is
(A) x + y = 0
(B) x – y = 0
(C) x + y +1 = 0
(D) x – y = 0
Question 23. The normal to the curve x2 = 4y passing (1,2) is
(A) x + y = 3
(B) x – y = 3
(C) x + y = 1
( D) x – y = 1
Question 24. The points on the curve 9y2 = x3, where the normal to the
curve makes equal intercepts with the axes are
(A) 4, 8 3
(B) 4, 8 3
(C) 4, 3 8
(D) 4, 3 8
:: Chapter 7 - Integral ::
EXERCISE
Question 1. Find the area of the region bounded by the curve y2 = x and the
lines x = 1, x = 4 and the x-axis.
Question 2. Find the area of the region bounded by y2 = 9x, x = 2, x = 4 and
the x-axis in the first quadrant. Fig
Question 3. Find the area of the region bounded by x2 = 4y, y = 2, y = 4 and
the y-axis in the first quadrant.
Question 4. Find the area of the region bounded by the ellipse 2 2 1 16 9 x y
+ = .
Question 5. Find the area of the region bounded by the ellipse 2 2 1 4 9 x y
+ = .
Question 6. Find the area of the region in the first quadrant enclosed by
x-axis, line x = 3 y and the circle x2 + y2 = 4.
Question 7. Find the area of the smaller part of the circle x2 + y2 = a2 cut
off by the line 2 x= a .
Question 8. The area between x = y2 and x = 4 is divided into two equal parts
by the line x = a, find the value of a.
Question 9. Find the area of the region bounded by the parabola y = x2 and y
= x .
Question 10. Find the area bounded by the curve x2 = 4y and the line x = 4y –
2.
Question 11. Find the area of the region bounded by the curve y2 = 4x and the
line x = 3. Choose the correct answer in the following Exercises 12 and 13.
Question 12. Area lying in the first quadrant and bounded by the circle x2
+ y2 = 4 and the lines x = 0 and x = 2 is
(A) π
(B) 2 π
(C) 3 π
(D) 4 π
Question 13. Area of the region bounded by the curve y2 = 4x, y-axis and
the line y = 3 is
(A) 2
(B) 9 4
(C) 9 3
(D) 9 2
EXERCISE
Question 1. Find the area of the circle 4x2 + 4y2 = 9 which is interior to
the parabola x2 = 4y.
Question 2. Find the area bounded by curves (x – 1)2 + y2 = 1 and x2 + y2 =
1.
Question 3. Find the area of the region bounded by the curves y = x2 + 2, y =
x, x = 0 and x = 3.
Question 4. Using integration find the area of region bounded by the triangle
whose vertices are (– 1, 0), (1, 3) and (3, 2).
Question 5. Using integration find the area of the triangular region whose
sides have the equations y = 2x + 1, y = 3x + 1 and x =
Question 4.Choose the correct answer in the following exercises 6 and 7.
Question 6. Smaller area enclosed by the circle x2 + y2 = 4 and the line x
+ y = 2 is
(A) 2 (π – 2)
(B) π – 2
(C) 2π – 1
(D) 2 (π + 2)
Question 7. Area lying between the curves y2 = 4x and y = 2x is
(A) 2 3
(B) 1 3
(C) 1 4
(D) 3 4
Miscellaneous Exercise on Chapter
Question 1. Find the area under the given curves and given lines:
(i) y = x2, x = 1, x = 2 and x-axis
(ii) y = x4, x = 1, x = 5 and x-axis
Question 2. Find the area between the curves y = x and y = x2.
Question 3. Find the area of the region lying in the first quadrant and
bounded by y = 4x2, x = 0, y = 1 and y = 4.
Question 4. Sketch the graph of y = x + 3 and evaluate 0 6 3 − ∫ x + dx .
Question 5. Find the area bounded by the curve y = sin x between x = 0 and x
= 2π.
Question 6. Find the area enclosed between the parabola y2 = 4ax and the line
y = mx.
Question 7. Find the area enclosed by the parabola 4y = 3x2 and the line 2y =
3x + 12.
Question 8. Find the area of the smaller region bounded by the ellipse 2 2 1
9 4 x + y = and the line 1 3 2 x y + = .
Question 9. Find the area of the smaller region bounded by the ellipse 2 2 2
2 x y 1 a b + = and the line 1 x y a b + = .
Question 10. Find the area of the region enclosed by the parabola x2 = y, the
line y = x + 2 and the x-axis.
Question 11. Using the method of integration find the area bounded by the
curve x + y = 1 . [Hint: The required region is bounded by lines x + y = 1, x– y
= 1, – x + y = 1 and – x – y = 1].
Question 12. Find the area bounded by curves {(x, y) : y ≥ x2 and y = | x |}.
Question 13. Using the method of integration find the area of the triangle
ABC, coordinates of whose vertices are A(2, 0), B (4, 5) and C (6, 3).
Question 14. Using the method of integration find the area of the region
bounded by lines: 2x + y = 4, 3x – 2y = 6 and x – 3y + 5 = 0
Question 15. Find the area of the region {(x, y) : y2 ≤ 4x, 4x2 + 4y2 ≤ 9}
Choose the correct answer in the following Exercises from 16 to 20.
Question 16. Area bounded by the curve y = x3, the x-axis and the
ordinates x = – 2 and x = 1 is
(A) – 9
(B) 15 4 −
(C) 15 4
(D) 17 4
Question 17. The area bounded by the curve y = x | x | , x-axis and the
ordinates x = – 1 and x = 1 is given by
(A) 0
(B) 1 3
(C) 2 3
(D) 4 3 [Hint : y = x2 if x > 0 and y = – x2 if x < 0].
Question 18. The area of the circle x2 + y2 = 16 exterior to the parabola
y2 = 6x is
(A) 4 (4 3) 3 π −
(B) 4 (4 3) 3 π +
(C) 4 (8 3) 3 π −
(D) 4 (8 3) 3 π +
Question 19. The area bounded by the y-axis, y = cos x and y = sin x when
0 2 x π ≤ ≤ is
(A) 2 ( 2 −1)
(B) 2 −1
(C) 2 +1
(D) 2
:: Chapter 8 - Application Of Integrals ::
EXERCISE
1. Find the area of the region bounded by the curve y^2 =x and
the lines x = 1 , x = 4 and the x axis
2.Find the area of the region bounded by y^2 = 9x, x=2, x =4 and
the x axis in the first quadrant.
3. Find the area of the region bounded by x^2 = 4y, y = 2, y = 4
and the y-axis in the first quadrant.
Find the equation of the region bounded by the ellipse x^2/16 +
y^2/9 =1
Find the equation of the region bounded by the ellipse x^2/4 +
y^2/9 =1
6. find the area of the region in the first quadrant enclosed by
x axis, line x =root 3 y and the circle x^2 + y^2 = 4
7.Area between x=y2 and x=4 is divided in two equal parts by the
line x = a, find the value of a
8. The area between x^2 = y and x = 4 is divided into two equal
parts by the line x = a, find the value of a.
9. Find the area of the region bounded by the parabola y = x^2
and y= |x|\
10. Find the area bounded by the curve x^2 =4y and the line x =
4y- 2
11. Find the area of the region bounded by the curve y2 = 4x and
the line x = 3.
12. Area lying in the first quadrant and bounded by the circle
x2 + y = 4 and the lines x = 0 and x = 2 is 2
13. Area of the region bounded by the curve y^2 =4x , y axis and
the line y=3 is
EXERCISE
1. Find the area of the circle 4x^2 + 4y^2 = 9 which is interior
to the parabola x^2 =4y
2. Find the area bounded by curves (x – 1)^2 + y^2 = 1 and x^2 +
y^2 = 1
3.Find the area of the region bounded by the curves y= x^2 + 2 ,
y=x , x =0 and x = 3
4.Using integration find the area of region bounded by the
triangle whose vertices are (– 1, 0), (1, 3) and (3, 2).
5. Using integration find the area of the triangular region
whose sides have the equations y = 2x + 1, y = 3x + 1 and x = 4.
6. Smaller area enclosed by the circle x^2 +y^2 = 4 and the
lines x + y = 2 is (A) 2 (π – 2) (B) π – 2 (C) 2π – 1 (D) 2 (π + 2)
7. Area lying between the curves y^2 = 4x and y = 2x is
Miscellaneous Solutions
1. Find the area under the given curves and given lines (i) y =
x^2 , x=1 , x= 2 and x axis (ii) y = x^4 , x=1 , x= 5 and x axis
2. Find the area between the curves y = x and y = x^2
3.Find the area of the region lying in the first quadrant and
bounded by y = 4x^2, x=0, y=1 and y= 4
4. Sketch the graph of y = x + 3 and evaluate integration limits
6 to 0 of x + 3 dx
5. Find the area bounded by the curve y = sin x between x = 0
and x = 2π.
6. Find the area enclosed between the parabola y^2 = 4ax and the
line y =mx
7. Find the area enclosed by the parabola 4y = 3x^2 and the line
2y = 3x + 12 using integration to find area,
8. Find the area of the smaller region bounded by the ellipse
x^2/9 + y^2/4 = 1 and the line x/3 + y/2 =1
:: Chapter 9 - Differential Equations ::

EXERCISE 9.2
In each of the Exercises 1 to 10 verify that the given functions (explicit or
implicit) is a solution of the corresponding differential equation:
Question 1. y = ex + 1 : y″ – y′ = 0
Question 2. y = x2 + 2x + C : y′ – 2x – 2 = 0
Question 3. y = cos x + C : y′ + sin x = 0
Question 4. y = 1+ x2 : y′ = 1 2 xy + x
Question 5. y = Ax : xy′ = y (x ≠ 0)
Question 6. y = x sin x : xy′ = y + x x2 − y2 (x ≠ 0 and x
> y or x < – y)
Question 7. xy = log y + C : y′ = 2 1 y − xy (xy ≠ 1)
Question 8. y – cos y = x : (y sin y + cos y + x) y′ = y
Question 9. x + y = tan–1y : y2 y′ + y2 + 1 = 0
Question 10. y = a2
− x2 x ∈ (–a, a) : x + y dy dx = 0 (y ≠ 0)
Question 11. The number of arbitrary constants in the general solution of a
differential equation of fourth order are:
(A) 0
(B) 2
(C) 3
(D) 4
Question 12. The number of arbitrary constants in the particular solution of a
differential equation of third order are:
(A) 3
(B) 2
(C) 1
(D) 0
EXERCISE 9.3
In each of the Exercises 1 to 5, form a differential equation representing
the given family of curves by eliminating arbitrary constants a and b.
Question 1. x y 1 a b + =
Question 2. y2 = a (b2 – x2)
Question 3. y = a e3x + b e– 2x
Question 4. y = e2x (a + bx)
Question 5. y = ex (a cos x + b sin x)
Question 6. Form the differential equation of the family of circles touching the
y-axis at origin.
Question 7. Form the differential equation of the family of parabolas having
vertex at origin and axis along positive y-axis.
Question 8. Form the differential equation of the family of ellipses having foci
on y-axis and centre at origin.
Question 9. Form the differential equation of the family of hyperbolas having
foci on x-axis and centre at origin.
Question 10. Form the differential equation of the family of circles having
centre on y-axis and radius 3 units.
Question 11. Which of the following differential equations has y = c1 ex + c2
e–x as the general solution?
(A) 2 2 d y y 0 dx + =
(B) 2 2 d y y 0 dx − =
(C) 2 2 d y 1 0 dx + =
(D) 2 2 d y 1 0 dx − =
Question 12. Which of the following differential equations has y = x as one
of its particular solution?
(A) 2 2 2 d y x dy xy x dx dx − + =
(B) 2 2 d y x dy xy x dx dx + + =
(C) 2 2 2 d y x dy xy 0 dx dx − + =
(D) 2 2 d y x dy xy 0 dx dx |
EXERCISE 9.4
EXERCISE 9.3
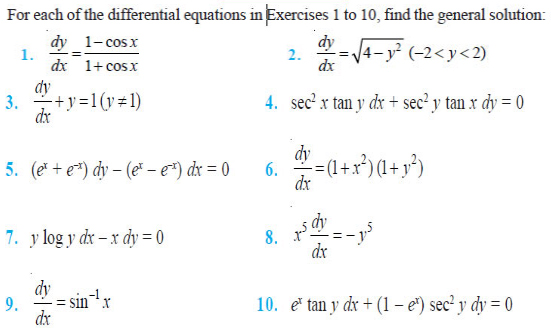

Question 17. Find the equation of a curve passing through the
point (0, –2) given that at any point (x, y) on the curve, the product of the
slope of its tangent and y coordinate of the point is equal to the x coordinate
of the point.
Question 18. At any point (x, y) of a curve, the slope of the tangent is twice
the slope of the line segment joining the point of contact to the point (– 4,
–3). Find the equation of the curve given that it passes through (–2, 1).
Question 19. The volume of spherical balloon being inflated changes at a
constant rate. If initially its radius is 3 units and after 3 seconds it is 6
units. Find the radius of balloon after t seconds.
Question 20. In a bank, principal increases continuously at the rate of r% per
year. Find the value of r if Rs 100 double itself in 10 years (loge2 = 0.6931).
Question 21. In a bank, principal increases continuously at the rate of 5% per
year. An amount of Rs 1000 is deposited with this bank, how much will it worth
after 10 years (e0.5 = 1.648).
Question 22. In a culture, the bacteria count is 1,00,000. The number is
increased by 10% in 2 hours. In how many hours will the count reach 2,00,000, if
the rate of growth of bacteria is proportional to the number present?
Question 23. The general solution of the differential equation dy ex y dx = + is
(A) ex + e–y = C (B) ex + ey = C (C) e–x + ey = C (D) e–x + e–y = C

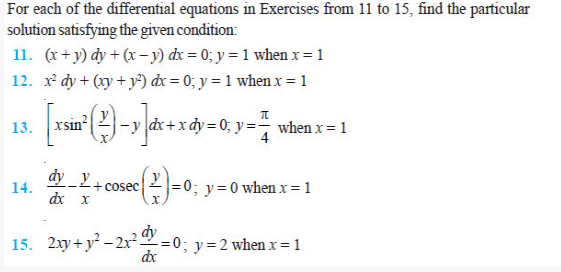
Question 16. A homogeneous differential equation of the from
dx h x dy y = can be solved by making the substitution.
(A) y = vx
(B) v = yx
(C) x = vy
(D) x = v
Question 17. Which of the following is a homogeneous differential equation?
(A) (4x + 6y + 5) dy – (3y + 2x + 4) dx = 0
(B) (xy) dx – (x3 + y3) dy = 0
(C) (x3 + 2y2) dx + 2xy dy = 0
(D) y2 dx + (x2 – xy – y2) dy = 0


Miscellaneous Exercise on Chapter 9
Question 1. For each of the differential equations given
below, indicate its order and degree (if defined).
(i) 2 2 2 d y 5x dy 6y log x dx dx +
(ii) 3 2 dy 4 dy 7 y sin x dx dx
(iii) 4 3 4 3 d y sin d y 0 dx dx
Question 2. For each of the exercises given below, verify that the given
function (implicit or explicit) is a solution of the corresponding differential
equation.
(i) y = a ex + b e–x + x2 : 2 2 2 x d y 2 dy xy x 2 0 dx dx + − + − =
(ii) y = ex (a cos x + b sin x) : 2 2 d y 2 dy 2y 0 dx dx − + =
(iii) y = x sin 3x : 2 2 d y 9y 6cos3x 0 dx + − =
(iv) x2 = 2y2 log y : (x2 y2 ) dy xy 0 dx + − =
Question 3. Form the differential equation representing the family of curves
given by (x – a)2 + 2y2 = a2, where a is an arbitrary constant.
Question 4. Prove that x2 – y2 = c (x2 + y2)2 is the general solution of
differential equation (x3 – 3x y2) dx = (y3 – 3x2y) dy, where c is a parameter.
Question 5. Form the differential equation of the family of circles in the first
quadrant which touch the coordinate axes.
Question 6. Find the general solution of the differential equation 2 2 1 0 1 dy
y dx x − + = − .
Question 7. Show that the general solution of the differential equation 2 2 1 0
1 dy y y dx x x + + + = + + is given by (x + y + 1) = A (1 – x – y – 2xy), where
A is parameter.
Question 8. Find the equation of the curve passing through the point 0, 4 whose
differential equation is sin x cos y dx + cos x sin y dy = 0.
Question 9. Find the particular solution of the differential equation (1 + e2x)
dy + (1 + y2) ex dx = 0, given that y = 1 when x = 0.
Question 10. Solve the differential equation 2 ( 0) x x y e ydx x e y y dy y ≠ .
Question 11. Find a particular solution of the differential equation (x – y) (dx
+ dy) = dx – dy, given that y = –1, when x = 0. (Hint: put x – y = t)
Question 12. Solve the differential equation 2 1( 0) x e y dxx x x dy.
Question 13. Find a particular solution of the differential equation cot dy y x
dx + = 4x cosec x (x ≠ 0), given that y = 0 when 2 x π = .
Question 14. Find a particular solution of the differential equation (x + 1) dy
dx = 2 e–y – 1, given that y = 0 when x = 0.
Question 15. The population of a village increases continuously at the rate
proportional to the number of its inhabitants present at any time. If the
population of the village was 20, 000 in 1999 and 25000 in the year 2004, what
will be the population of the village in 2009?
Question 16. The general solution of the differential equation y dx x dy 0 y
− = is
(A) xy = C
(B) x = Cy2
(C) y = Cx
(D) y = Cx2
Question 17. The general solution of a differential equation of the type P1
Q1 dx x dy + = is
(A) P1 ( P1 ) Q1 C dy dy y e∫ = ∫ e∫ dy +
(B) P1 ( P1 ) . Q1 C dx dx y e∫ = ∫ e∫ dx +
(C) P1 ( P1 ) Q1 C dy dy x e∫ = ∫ e∫ dy +
(D) P1 ( P1 ) Q1 C dx dx x e∫ = ∫ e∫ dx +
Question 18. The general solution of the differential equation ex dy + (y ex
+ 2x) dx = 0 is
(A) x ey + x2 = C
(B) x ey + y2 = C
(C) y ex + x2 = C
(D) y ey + x2 = C